
Cреднее арифметическое значение (далее по тексту — среднее), пожалуй, наиболее популярный статистический параметр. Этим понятием пользуются повсеместно — начиная от поговорки «средняя температура по больнице» и кончая серьезными научными трудами. Однако, как ни странно, среднее значение — коварное понятие, часто вводящее в заблуждение, вместо того чтобы придавать четкость изложению и вносить ясность.
Если говорить о научной работе, то статистический анализ данных применяется почти во всех прикладных науках, даже и в гуманитарных (например, психологии). Среднее значение вычисляется для признаков, измеряемых в так называемых непрерывных шкалах. Такими признаками являются, например, концентрации веществ в сыворотке крови, рост, вес, возраст. Среднее арифметическое можно легко вычислить, и этому учат еще в средней школе. Однако (в соответствии с положениями математической статистики) среднее значение является адекватной мерой центральной тенденции в выборке только в случае нормального (гауссова) распределения признака (рис. 1).
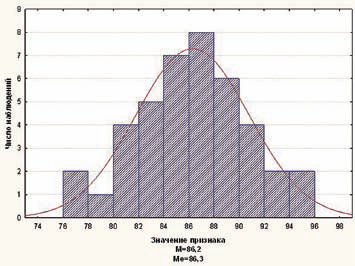
В случае же отклонения распределения от нормального закона среднее значение использовать некорректно, так как оно является слишком чувствительным параметром к так называемым «выбросам» — нехарактерным для изучаемой выборки,слишком большим или слишком малым значением (рис. 2). В этом случае для характеристики центральной тенденции в выборке должен применяться другой параметр — медиана. Медиана — это значение признака, справа и слева от которого находится равное число наблюдений (по 50%). Этот параметр (в отличие от среднего значения) устойчив к «выбросам». Заметим также,что медиана может использоваться и в случае нормального распределения — в этом случае медиана совпадает со средним значением.
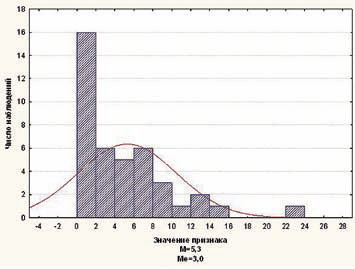
Для того, чтобы узнать, является ли распределение признака в выборке нормальным (гауссовым) или нет, т.е. для того, чтобы узнать, какой из параметров следует применять (среднее значение или медиану), существуют специальные статистические тесты.
Приведем пример. Скорость оседания эритроцитов в группе пациентов, недавно перенесших пневмонию, — 3, 5, 5, 7, 11, 12, 16, 16, 21, 42, 58. Среднее значение для этой выборки равно 17,8, медиана — 12. Распределение (по тесту Шапиро—Уилка) нормальным не является (рис. 3), поэтому использовать надо медиану.
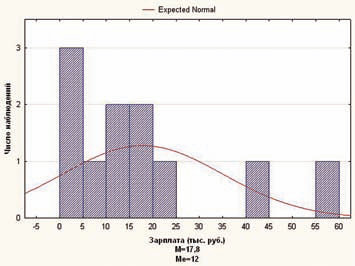
Как ни странно, но в некоторых областях экономики сторонний наблюдатель не может заметить хоть какого-то следа корректного применения математической статистики. Так, нам постоянно говорят о средней зарплате (например, в НИИ), и эти числа обычно удивляют не только рядовых сотрудников, но и руководителей подразделений (ныне называемых «менеджерами среднего звена»). Мы удивляемся, что средняя зарплата в Москве — 40 тыс. руб., но, конечно, понимаем, что нас «усреднили» с олигархами. Вот пример из жизни научных работников: зарплаты сотрудников лаборатории (тыс. руб.) — 3, 5, 5, 7, 11, 12, 16, 16, 21, 42, 58. Среднее значение — 17,8, медиана — 12. Согласитесь, что это разные числа!
Конечно, нельзя исключить, что замалчивание свойств среднего — лукавство, так как руководству всегда выгоднее представить ситуацию с зарплатой сотрудников лучше, чем она есть на самом деле.
Не пора ли научному сообществу призвать наших руководителей прекратить некорректное использование математической статистики?
Ольга Реброва,
докт. мед. наук, вице-президент
МОО «Общество специалистов доказательной медицины»
РОЭ идеально коррелирует с зарплатами ))
Низя,уменьшат выборку!
Статья понравилась.
Было бы еще лучше, если бы в примере приводились реальные цифры по зарплатам :)
Если один съел курицу, а второй не съел ничего, то в среднем эти двое съели по пол-курицы.
Старый-старый, бородатый анекдот про то же самое.
Есть еще более изящный «закон 20/80»:
20% людей выпивают 80% пива.
Касается не только пива, но и работы, и зарплаты… И солнца, и счастья…
Самое интересное — это то что распределение скорости оседания эритроцитов в точности такое же как зарплаты сотрудников лаборатории.
Совпадение? Не думаю.
Среднее элементарно проще подсчитать.
К сожалению, в статистике есть много лазеек для подгонки данных под определенные нужды, начиная от выборки групп, количества исследуемых в разных группах, параметов включения и исключения и пр. Медиана и среднее арифметическое — это просто числа, которые образуются в результате специально отобранной группы наблюдений. Статистика — неточная наука!
А есть более точная чем статистика?
Отличная статья. Благодарю Автора!
Спасибо за статью. Опубликовал у себя на ленте в facebook.