Охотники за квадратами

Добровольные распределен­ные вычисле­ния — относительно новый способ расчетов, в которых компьютеры частных лиц объединяются в специальных проектах для решения масштабных (чаще всего на­учных) задач. После подключения к проек­ту вычисления выполняются автоматически, не причиняя участнику никаких неудобств (используются только свободные ресурсы компьютеров). Хотя идея подобной орга­низации вычислений появилась довольно давно, первым добровольным проектом с современными чертами был стартовавший в 1996 году проект GIMPS, предназначен­ный для поиска простых чисел Мерсенна. В 1999 году специалистами из Беркли был запущен проект SETI@home, задачей кото­рого был поиск радиосигналов внеземных цивилизаций. В 2002 году на основе SETI@ home была разработана открытая платфор­ма BOINC, которая значительно упростила создание новых проектов добровольных вычислений. На данный момент активно работают более 70 проектов, большинство из которых основано на BOINC. Суммарная производительность всех проектов сейчас составляет более 7 петафлопс, с помощью этих колоссальных ресурсов каждый год де­лаются научные открытия в многих областях. Среди важных результатов стоит упомянуть открытие нескольких десятков радиопуль­саров в проекте Einstein@home и откры­тие ряда простых чисел специального вида и арифметических прогрессий из простых чисел в проекте PrimeGrid.

Успехи любого проекта были бы невоз­можны без наличия в нем достаточных компьютерных мощностей. Но посколь­ку количество проектов «@home» при­ближается уже к сотне и каждый их них борется за пользователей и их компью­теры, то конкуренция из-за вычислитель­ных ресурсов идет достаточно серьезная.

Российские кранчеры (так называют себя участники проектов добровольных вычис­лений) давно истосковались по отечествен­ным проектам, которые можно пересчитать по пальцам. Конечно, интересно участвовать в поиске новых лекарств (проект Rosetta@home) или помогать в расчетах магнитной системы Большого адронного коллайдера (проект LHC@home). Однако вдвойне при­ятнее было бы оказать посильную помощь ученым-соотечественникам. И вот, в сентя­бре 2011 года появился российский проект SAT@home, который сразу привлек внима­ние отечественных кранчеров.

SAT (сокращенно от Satisfability) — это задача доказательства выполнимости булевых фор­мул специального вида. SAT-подход состоит в сведении исходных задач к SAT-задачам с их последующим решением специальны­ми решателями. С помощью SAT-подхода можно решать задачи верификации, крип­тографии, комбинаторики, биоинформати­ки. В лаборатории дискретного анализа и прикладной логики Института динамики си­стем и теории управления Сибирского от­деления РАН (ИДСТУ СО РАН) SAT-подход активно развивается. В частности, созданы программные комплексы, с помощью кото­рых к SAT сведены задачи анализа динами­ки поведения генных сетей, задачи крипто­анализа генераторов ключевого потока, а также задачи поиска новых комбинатор­ных структур (в первую очередь — систем латинских квадратов).

Получаемые SAT-задачи довольно слож­ные, но они допускают разбиение на неза­висимые друг от друга подзадачи, что по­зволяет использовать для их решения не только суперкомпьютеры, но и гриды. В ла­боратории были разработаны и успешно использованы на суперкомпьютерах па­раллельные SAT-решатели, но для обра­ботки некоторых классов задач не хва­тало вычислительных ресурсов. Именно поэтому в 2011 году Институтом динами­ки систем и теории управления Сибирско­го отделения РАН (Иркутск) в сотрудни­честве с Институтом системного анализа РАН (Москва) был запущен проект добро­вольных распределенных вычислений SAT@home. Сначала производительность SAT@home была как у небольшого ком­пьютерного класса, но уже к середине 2012 года она приблизилась к показате­лям из списка ТОП-50 суперкомпьюте­ров СНГ. Но, в отличие от обычного супер­компьютера, ресурсы проекта работают в режиме 24/7 на одну масштабную зада­чу. По состоянию на 10 ноября 2012 го­да, в проекте было зарегистрировано 3152 участника из 92 стран, которые подключили 8277 компьютеров. На данный момент рос­сийские добровольцы суммарно выполнили 42% вычислений в проекте, добровольцы из США выполнили 17%, а из Германии — 11%. У остальных стран доля выполненных вы­числений значительно меньше. Средняя производительность проекта составляет 2,3 терафлопс.

В мае 2012 года в проекте был проведен полугодовой эксперимент, направленный на решение 10 задач исследования стойкости системы шифрования A5/1, которые не ре­шаются известными стандартными спосо­бами (с помощью rainbow-таблиц). В каж­дой задаче нужно было найти неизвестное начальное заполнение генератора ключе­вого потока, по сути это задача обращения функции — по известному выходному зна­чению надо найти входное значение. Все 10 задач были успешно решены в проек­те. Сейчас в SAT@home запущен экспери­мент, направленный на поиск пар и троек ортогональных латинских квадратов по­рядка 10. Латинский квадрат порядка n — это таблица n × n, заполненная n различ­ными символами таким образом, чтобы в каждой строке и в каждом столбце встре­чались все n символов (каждый по одно­му разу). Пара латинских квадратов одина­кового порядка называется ортогональной, если различны все упорядоченные пары символов (a,b), где a — символ в некоторой клетке первого латинского квадрата, а b — символ в той же клетке второго латинско­го квадрата. Латинские квадраты приме­няются в различных прикладных областях, таких как криптография (несколько шиф­ров построены на специально подобран­ных латинских квадратах), проведение экспериментов (использование пар орто­гональных латинских квадратов позволя­ет сократить перебор вариантов), а также в кодировании информации (система по­парно ортогональных латинских квадра­тов позволяет составить правильный по­рядок передачи данных).

Руководители российского проекта SAT@ home изначально установили тесный кон­такт с российским сообществом любите­лей добровольных распределенных вы­числений. Ведутся активные дискуссии на форуме сайта BOINC.RU, обеспечивая обратную связь между организаторами и участниками проекта. И это показало свою эффективность. Для ускорения ра­боты проекта одна из российских команд организовала на статистическом сайте BOINCstats.com соревнования в проекте SAT@home, в которых приняли участие 16 команд и более 200 участников из раз­ных стран. Суть подобных виртуальных со­ревнований состоит в том, что в течение ограниченного периода времени (обыч­но 7 дней) статистика для зарегистриро­ванных участников обновляется каждые 15 минут (а не раз в сутки, как обычно).

Поэтому следить за изменением со­ревновательной ситуации можно практически в реальном мас­штабе времени. Победителем считается участник или команда, получившие наи­большее количество начисляемых баллов (кредитов) за отведенное время, т.е. об­работавшие наибольшее число заданий проекта. В итоге команды и участники ста­раются активизироваться, подключить до­полнительные вычислительные мощности для более успешного выступления. Про­ект при этом получает мощный прирост производительности и одновременно се­рьезную нагрузку на сервер, так как резко возрастает количество подключений для получения заданий и отправки результа­тов. Ну а участники взамен имеют сорев­новательный азарт, приток адреналина и моральное удовлетворение.

Данное соревнование было посвяще­но годовщине проекта. Но поскольку оно проводилось на месяц позднее «юбилея» (из-за запуска в проекте нового экспе­римента в нем некоторое время не было заданий), то получило в шутку название «Счастливая «чертова дюжина»» («Happy «baker’s dozen»»).

Соревнование проходило в очень напря­женной борьбе, которую вели между со­бой команды «Russia Team» и «Astronomy. Ru Forum». Первые два дня команды шли «ноздря в ноздрю», попеременно занимая лидирующую позицию. При этом, если «Rus­sia Team» сделала ставку на привлечение и активизацию максимального числа сво­их участников (77 человек), то «Astronomy. Ru Forum» удалось победить с огромным итоговым отрывом благодаря участнику из Туркменистана с ником tanos. Ему уда­лось привлечь к работе в проекте более 200 компьютеров и не только обеспечить своей команде победу в этой виртуальной гонке, но и заслуженно стать одним из ав­торов двух найденных решений.

Идея запуска соревнования полно­стью себя оправдала. Была достигну­та производительность 6,3 терафлопс, что стало историческим максимумом за 13 месяцев работы проекта (преды­дущий рекорд был 4,7 терафлопс, он так­же был достигнут во время подобного со­ревнования в 2011 году). График произ­водительности проекта за последний год представлен ниже. Последний пик соот­ветствует проведенному недавно сорев­нованию.

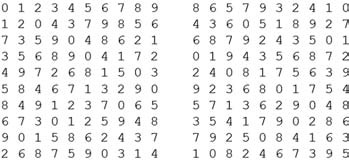
Однако главным результатом соревно­вания стало нахождение двух пар диаго­нальных ортогональных латинских ква­дратов порядка 10. Ниже приведена одна из найденных пар.

В этой паре в каждом квадрате каждая строка, столбец а также главная и побочная диагонали состоят из чисел от 0 до 9, при этом ни одно число не повторяется. Имен­но поэтому каждый из этих квадратов яв­ляется латинским и диагональным. Условие ортогональности выполняется, так как если наложить первый квадрат на второй, то ни одна из полученных пар чисел не будет повторять­ся (для первой ячейки первой строки это пара 08, для второй ячейки — 16 и т. д.). Сейчас мы пытаем­ся оценить важность полученных нами результа­тов. С одной стороны, ранее были известны только три пары диагональных ортогональных латинских квадратов, они были опубликованы в 1992 году [1]. С другой стороны, главный результат статьи [1] со­стоял в доказательстве существования таких пар, и авторы не ставили перед собой задачу найти их как можно больше.

В перспективе в рамках проекта планируется ор­ганизация нового масштабного вычислительного эксперимента, направленного на поиск тройки по­парно ортогональных латинских квадратов поряд­ка 10. На текущий момент 10 — это минимальный порядок, для которого неизвестно существование такой тройки. Эта задача очень сложная, несколь­ко научных коллективов по всему миру пытаются решить ее уже несколько десятилетий. Вообще до­бровольные вычисления оказались очень хорошим подспорьем для проведения научных эксперимен­тов. К тому же здесь идет постоянное живое обще­ние с участниками, что очень полезно для развития и оптимизации как проекта, так и всего процесса научного исследования.

1. Brown et al. Completion of the Spectrum of Orthogonal Diagonal Latin Squares. Lecture notes in pure and applied mathematics. 1992. Vol. 139. Pp 43–49.