Критерии оценки результативности фундаментальных научных исследований можно разделить на качественные и количественные показатели. Еще с советских времен отечественные ученые привыкли именно к качественным показателям – научные регалии (ученые степени и звания), отзывы экспертов (оппонирование диссертаций, рецензирование статей, экспертиза заявок на гранты), научное признание (научные премии и награды) и т.д. Экспертная оценка – очень трудная и зачастую необъективная вещь (особенно в нашей стране), поэтому были разработаны количественные наукометрические показатели. Основные из них – это число статей, индекс цитирования, индекс Хирша, импакт-фактор. В современной России при оценке результативности науки наукометрические показатели используются все шире. Например, в конкурсной документации для участия в Федеральной целевой программе «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014-2020 годы» необходимо указывать число публикаций и число цитирований за последние пять лет, а также индекс Хирша по данным трех основных баз данных: Web of Science, Scopus и РИНЦ. Определенные требования к числу статей в индексируемых в базах данных Web of Science и Scopus предъявляет Российский научный фонд. В Российской академии наук разработан комплексный индикатор – ПРНД, определяемый на основе учета числа статей, импакт-факторов журналов и др. Созданы базы данных, содержащие основные наукометрические показатели деятельности отечественных ученых: проект «Кто есть кто в российской науке» и министерская «Карта российской науки».
Следует признать, что количественные наукометрические показатели абсолютно беспристрастны, но и они далеко не идеальны. Импакт-фактора никак не отражает качества отдельно взятой работы, опубликованной в журнале, а характеризует журнал в целом. Можно опубликовать статью в высокоимпактном журнале, которая не получит ни одного цитирования. Индекс цитирования в свою очередь не учитывает в явном виде уровень журналов, в которых опубликованы цитируемые статьи. Относительно этого индекса статьи, опубликованные в известных признанных изданиях с высоким импакт-фактором и статьи в низкопробных журналах с низким или нулевым импакт-фактором, но процитированные одинаковое число раз, эквиваленты. Это значит, что научные сотрудники за счет договорного перекрестного цитирования статей друг друга, публикуемых в нечитаемых никем, кроме них самих, «местечковых» журналах с низким или нулевым импакт-фактором, могут нагнать себе довольно значительные индексы цитирования. Число статей уравнивает публикации в известных признанных изданиях с самыми высокими импакт-факторами и статьи в мало кому известных журналах с низкими или даже нулевыми импакт-факторами. Кроме того, статьи могут по-разному цитироваться, что также говорит об их неравнозначности, но никак не отражается этим показателем. Считается, что индекс Хирша на данный момент дает самую адекватную оценку научной результативности исследователя по сравнению с такими простыми характеристиками, как общее число статей или индекс цитирования. Однако и он не лишен недостатков, например, он явно никак не учитывает уровень научного издания (импакт-фактор), в которых опубликованы статьи. Кроме того, индекс Хирша плохо учитывает наиболее важные работы с максимальной цитируемостью. Здесь приведена лишь небольшая часть недостатков основных наукометрических показателей. Более полный перечень с реальными примерами можно найти в работе [1]. Рассмотренные недостатки каждого из наукометрических показателей в отдельности, а также неудобство их совместного использования стимулируют поиск других количественных критериев [1]. Ниже предложен новый интегральный показатель, устраняющий вышеперечисленные недостатки основных наукометрических показателей.
Интегральный наукометрический показатель вычисляется по формуле:
здесь n – число статей, fi – импакт-факторы журналов, в которых опубликованы статьи, ci – число цитирований статьи, опубликованной в журнале с импакт-фактором fi. Оценка результативности фундаментальных научных исследований с использованием каждого наукометрического показателя, входящего в формулу (1), по отдельности иногда бывает некорректной. Рассматривать одновременно несколько величин просто неудобно. Поэтому введение в практику оценки результативности фундаментальных научных исследований интегрального наукометрического показателя может быть целесообразно потому, что он нивелирует часть недостатков известных наукометрических показателей.
Для наглядности проведем характеристику интегрального наукометрического показателя на мысленном примере сравнения результативности научных исследований вымышленных персонажей. Рассмотрим трех научных сотрудников A, B, C, имеющих публикации, охарактеризованные в таблице 1. Заметим, что наукометрические показатели, указанные в таблице 1 вымышлены и могут значительно отличаться от аналогичных реальных показателей. Проведем сравнение исследователей A, B, C по каждому из наукометрических показателей.
Если в качестве критерия результативности исследований выбрать число публикаций n, то самым научно-продуктивным окажется последний исследователь C (с числом публикаций n=5), а наименее эффективным – первый, обозначенный буквой A (с числом публикаций n=3). Если же во внимание принять только индекс цитирования c, то научные результативности обоих сотрудников A и C окажутся эквивалентными (у обоих c=28). Наглядно видно, что лишь одного из параметров n или c явно недостаточно. При оценке научной результативности следует рассматривать одновременно оба этих количественных параметра. При этом кажется очевидным, что при равных индексах цитирования более успешным следует признать того, у кого больше число статей (при одинаковых значениях c), т.е. ученого, обозначенного буквой C.
Таблица 1. Характеристика публикаций вымышленных исследователей A, B, C
|
Научный сотрудник |
Импакт-факторы журналов fi и число цитирований каждой статьи ci |
Число статей n |
Индекс цитирования c |
Индекс Хирша h |
Средний импакт-фактор fa |
Интегральный наукометрический показатель k |
|
A |
f1=6, c1=5 f2=3, c2=3 f3=0, c3=20 |
3 |
28 |
3 |
3 |
39 |
|
B |
f1=10, c1=0 f2=1, c2=3 f3=1, c3=5 f4=0, c4=10 |
4 |
18 |
3 |
3 |
8 |
|
C |
f1=5, c1=20 f2=1, c2=3 f3=2, c3=0 f4=1, c4=5 f5=1, c5=0 |
5 |
28 |
3 |
2 |
108 |
Введем в рассмотрение исследователя B, который по числу статей n занимает промежуточную позицию (с числом публикаций n=4) между A и C. Индекс цитирования c сотрудника B оказывается равным 18, что заметно ниже аналогичного значения исследователей A и C. При сравнительной оценке научной результативности B и C никаких сомнений не возникает. У последнего ученого C (n=5, c=28) оба наукометрических показателя больше, чем у научного сотрудника B (n=4, c=18), а значит, научный результат его следует признать более весомым.
Совсем непростая ситуация возникает при сравнении научных достижений A и B. Если смотреть по числу статей, то более результативным окажется второй. Если же принять во внимание индекс цитирования, то напротив значимость результата первого оказывается выше. Здесь рассмотрение одновременно двух наукометрических показателя n и c не позволяет принять решение, чья результативность выше. Какой из критериев важнее, объективнее и честнее: число статей или индекс цитирования? Смысл у них совершенно разный и сравнивать, и выбирать из них некорректно. Первый характеризует активность и работоспособность самого исследователя, а второй – интерес к его работам со стороны коллег. Поэтому следует признать, что оба этих критерия важны. Естественным образом возникает необходимость ввести в рассмотрение третий показатель – индекс Хирша h, который учитывает, как число статей, так и их цитирование. Но, значения n и c в таблице 1 подобраны специально таким образом, чтобы индекс Хирша для всех трех научных сотрудников оказывается одинаковым (h=3). В расчете величины h не фигурирует импакт-фактор журналов f, в которых опубликованы статьи, хотя кажется очевидным, что результат, опубликованный в Nature (f=38.597) несравненно более значим, чем результат, опубликованный в Вестнике Московского университета. Серия 3. Физика. Астрономия (f=0.225). Поэтому необходимо принять во внимание и этот параметр тоже в виде среднего значения импакт-фактора fa по всем журналам, в которых опубликованы статьи. Но, значения n и f в таблице 1 подобраны специально таким образом, чтобы средние значения fa для исследователей A и B оказалось равны. Таким образом, складывается ситуация, что, несмотря на учет все четырех наукометрических показателей, надежного численного критерия результативности научных исследований, проводимых A и B, нет.
Более того, при введении в рассмотрение среднего импакт-фактора возникают дополнительные трудности в сравнении исследователей A и C. Выше при рассмотрении лишь двух наукометрических показателя (число статей и индекс цитирования) был сделан вывод о том, что научные результаты сотрудника C важнее, чем результаты его коллеги A. Так как у C число публикаций больше, чем у A при одинаковых значениях индексов цитирования и Хирша. Если же теперь принять во внимание средний импакт-фактор журналов, в который опубликованы научные результаты A и C, то оказывается, что напротив результаты сотрудника A важнее (fa=3), чем результаты его коллеги C (fa=2). Вновь возникает необходимость выбора, какой из двух наукометрических показателей важнее: число статей или средний импакт-фактор? И ответ вновь тот же: смысл у них совершенно разный и сравнивать, и выбирать из них некорректно.
Вышеописанный мысленный пример призван продемонстрировать, что распространенная практика использования даже нескольких наукометрических показателей не совсем корректна и удобна. Этим обусловлена необходимость введения в практику нового интегрального показателя k, рассчитываемого по формуле (1). При расчете величины k принимается во внимание основные наукометрические показатели. Расчет интегрального показателя k для вымышленных исследователей A, B, C приведен в последнем столбце таблицы 1. С помощью величины k можно однозначно оценивать результативность их научной работы. Из таблицы 1 видно, что интегральный показатель является ключевым в случае, когда прочие наукометрические показатели примерно близки.
Величина k имеет наглядную геометрическую интерпретацию (рисунок 1).

Рисунок 1. Наглядная геометрическая интерпретация интегрального наукометрического показателя k. Красные фигуры соответствуют научному сотруднику A, зеленые – B, синие – C (см. таблицу 1). Каждая фигура символизирует одну статью. Прямые линии отвечают статьям с нулевой цитируемостью или статьям, опубликованным в журналах с нулевым импакт-фактором. Цитируемость соответствует длине фигуры, импакт-фактор – высоте фигуры. Масштаб: 1 балл fi или ci эквивалентен 0.1 см длины
Каждое из слагаемых, входящих в сумму (1) представляет собой площадь прямоугольника со сторонами fi и ci. Т.е. каждая статья эквивалента прямоугольнику со сторонами fi и ci. Чем больше статей, тем больше прямоугольников, тем больше соответственно их суммарная площадь. Замечательная особенность интегрального наукометрического показателя k заключается в том, что он отсекает и не принимает в расчет малозначимые статьи, опубликованные в журналах с нулевым импакт-фактором (fi=0). Также не вносят вклада статьи, на которых никто не ссылается (ci=0). В обоих случая произведение fi∙ci=0. Геометрически это эквивалентно тому, что прямоугольник вырождается в прямую линию с нулевой площадью.
Из таблицы 1 видно, что для достижения высоких значений показателя k недостаточно писать много статей, пусть даже и высокоцитируемых. Нужно писать много высокоцитируемых статьей в хорошие высокоимпактные журналы.
Рассмотрим теперь примеры применения интегрального наукометрического показателя для оценки результативности фундаментальных научных исследований, проводимых реальными научными сотрудниками Института проблем химической физики РАН (таблица 2). Для расчета будем пользоваться наукометрическими данными РИНЦ.
Таблица 2. Наукометрические данные научных сотрудников Института проблем химической физики РАН по данным РИНЦ
|
№ |
Научный сотрудник |
Число статей n |
Индекс цитирования c |
Индекс Хирша h |
Средний импакт-фактор fa |
Интегральный наукометрический показатель k (округленный до целых) |
|
1. |
Дмитриев А.И., к.ф.-м.н., с.н.с. |
54 |
116 |
5 |
0.993 |
145 |
|
2. |
Кулагина Т.П., д.ф.-м.н., зав. лаб. |
37 |
120 |
5 |
0.511 |
41 |
|
3. |
Левченко А.В., к.х.н., с.н.с. |
55 |
236 |
8 |
1.062 |
220 |
|
4. |
Спицына Н.Г., к.х.н., с.н.с. |
44 |
277 |
8 |
0.574 |
73 |
|
5. |
Акимов А.В., к.ф.-м.н., с.н.с. |
77 |
556 |
12 |
2.551 |
1510 |
|
6. |
Михайлов А.И., д.х.н., г.н.с. |
229 |
876 |
11 |
0.678 |
469 |
В таблице 2 представлены наукометрические данные различных авторов, которые образуют три группы (первая группа – это исследователи под номерами 1 и 2, вторая – 3 и 4, третья – 5 и 6). В каждой группе по два сотрудника с близкими значениями индекса Хирша (в первой и второй группе также близки значения n и c). Поэтому могло бы показаться, что их научная результативность одинакова. Однако интегральный наукометрический показатель позволяет однозначно утверждать, что это совсем не так. Внутри каждой группы он различается приблизительно втрое при прочих приблизительно равных показателях. Кроме того, анализ третьей группы свидетельствует о том, что при близких значениях индекса Хирша, число статей и индекс цитирования являются некорректными показателями, так как дают ложные оценки результативности научной работы. Таблица 2 прямо свидетельствует о том, что мысленные примеры из таблицы 1 не являются надуманными. В практике оценки научной результативности имеют место ситуации, когда обходиться без интегрального наукометрического показателя очень трудно. Более того, игнорирование этого универсального показателя может приводить не только к грубым ошибкам, но и к совершенно абсурдным результатам.
А.И. Дмитриев,
Институт проблем химической физики РАН
1. http://eqworld.ipmnet.ru/ru/info/sci-edu/Polyanin_IndexH_2014.html
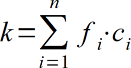
Сам недавно только думал о недостатках индекса Хирша. Интересные у вас размышления, только вот какова целевая аудитория? Если «учёные в принципе», то ТРВ, вероятно, не самый читаемый научный источник за пределами русскоязычного научного сообщества. Если «российские учёные», то зачем ещё один рейтинг для повышения ЧСВ? Чтобы руководству университетов было проще делать количественные выводы о производительности сотрудников и решать, кого следующим пустить в расход? Будьте уверены, как только появится возможность оценивать сотрудников по таким вот критериям, тяжкие настанут времена. Дело в том, что, вероятно, до определённого значения ИНП фактической разницы в «научном выходе» нет.
С другой стороны, допустим, ИНП — вещь полезная. Но вы сами в своей же статье указываете направления для махинаций. Скажем, работаю я среди учёных, кто публикуется в журналах с ИФ 1-3, но мне вдруг посчастливилось протолкнуть своё изыскание, допустим, в Biomacromolecules (5.371) или Macromolecules (5.521). Я прошу всех своих знакомых, работающих в моей области, ссылаться при каждой возможности на мою статью в этом журнале. Моё ЧСВ, вернее, ИНП, растёт в разы быстрее, чем ИНП моих коллег, манипулируемое тем же самым образом. А что будет, если я в JACS статью опубликую? Ну и так далее.
Следовательно, нужен ещё коэффициент учёта самоцитирований, как минимум. А то получится, что ты сделал открытие, оказавшее значимое влияние на всю твою последующую работу, но никому больше не интересное. Зато ИНП вон какой, «нас не догонят».
Все эти системы не лишены одних и тех же недостатков, к сожалению. Наверное, именно поэтому индекс Хирша и был принят на вооружение — при всей своей неточности, он отражает тренд, что более важно. Посмотрите, ваша же таблица реальных сотрудников даёт нам приблизительно такой же результат: самый классный сотрудник — Акимов. Догоняет — Михайлов. А что там на галёрке — так оно и не так важно в конечном счёте, ведь уже понятно, кого надо бы поощрить :)
К тому же, ИХ элементарен в своей логике подсчёта. Для подсчёта же ИНП необходимо всегда иметь список ИФ всех журналов, которые обновляются, а то и забывают обновляться, каждый год.
Интересно, но видно что работал химик, а не физик(шутка).
Что не учтено:
1) число соавторов (и даже их порядок играет роль, вспомни как пишется статья!!!)
2) фоновое слагаемое:
т.е. важен не только сам. имп фактор f, а величина (1+f);
и умножать его надо не просто на цитирование с, а на величину (1+Кс*с),
где Кс- коэффициент учета цитирования (разумно положить Кс=0.1).
ПОЯСНЯЮ:
Введение фонового слагаемого (1+..) отражает тот факт,
что публикация важна сама по себе, независимо от f и c.
Но, самое главное что не учел химик, это
3) экспертная значимость статьи.
А ее можно оценить только проведя дискуссию «в защиту публикации».
Например на спц. совете по защитам дисс-й.
Мы все хорошо знаем «придурковатость» рецензентов,
особенно в значимых журналах.
Там есть своя клановость.
И сначала надо попасть в обойму (при помощи уже маститых соавторов),
набраться багажа публикаций, а потом уж «трава не расти»,
т.е. берут все(да и опыт публикаций задает нужный авторский уровень)!!!
Короче,
в ТрВ, гайд-парке от 16.09.13г я предлагал гораздо более существенную методику
объективного оценивания публикационной активности, включающую процедуру «защиты» определенной совокупности публикаций и соответствующего индекса П.
Вот когда ты защитишь свои публикации,
то вместо спорных индексов будешь иметь соотв. уч. степень:
кандидат, младший доктор, доктор,старший доктор и тп.
(читай указанную выше ссылку), тогда по своей степени и будешь ценен..
Работать надо!!.
Не могу согласиться с логикой автора. Если статья в менее известном журнале набрала столько же цитирований, сколько статья в журнале, имеющим в десять раз больший тираж и читаемом куда более широкой аудиторией, то это успех, а не поражение. Поэтому нелогично умножать число цитирований на импакт-фактор журнала. Тот, кто публикуется в журналах с высоким импакт-фактором и так получает дополнительный бонус в виде того, что этот журнал больше читают, больше уважают и, следовательно, охотнее и чаще цитируют.
Если г-н Л. публикуется в более популярных и цитируемых журналах, чем г-жа С., написал больше статей, а общее число цитирований у него ниже, то почему мы должны оценивать его успехи выше, чем успехи г-жи С.? Мне кажется, что наоборот, в такой ситуации мы должы признать, что скорей всего цитируемость г-на Л. существенно ниже, чем у других работ из тех журналов, где он публикуется, и импакт-факторы этих журналов никак не характеризуют вклад г-на Л.
Ещё один недостаток предлагаемого подхода — это полное игнорирование количества соавторов, внёсших вклад в каждую из работ.
очень хорошая статья — хоть какая -то попытка создания объективного показателя (в отличие от вышекритикующих граждан, называющих себя «физиками»))))))))))
вызывает хохот..сразу видно, что это за «физик».
Правда, не знаю, похвала алкоголика может и не очень большой повод радоваться..
Разумеется, можно чтонть и подправить в предложенных оценках.
Только вот почему-то у критиков не было претензий к индексу Хирша, который не учитывал ни число соавторов, ни импакты журналов..
А теперь претензии появились)) Во вкус, видимо, вошли))
По поводу числа соавторов. Ну вот я, например, в качестве соавторов имею свой молодой научный коллектив, в котором все мои аспиранты и студенты. Иногда они не очень большой вклад вносят. Но им нужно расти. И наличие статей нужно позарез (например он методику отлаживает, не выгнать же его из аспирантуры за это на основании отсутствия статей?). Это прекрасно понимают квалифицированные коллеги как из РФ, так и из за рубежа. Ну давайте число соавторов учитывать (хотя ни один индекс, кроме министерских цифирей, нигде в мире этого не учитывал, и это сразу вдает ведомственную принадлежность критиканов).
Тогда я должен буду писать в статью только самого себя, так как я и измеряю сам все практически, и пишу сам…а молодых будем выкидывать — ждать пока сами напишут. Так чтоль?
Да и много дури в этом подходе есть. Типичной министерской дури, основанной на полном отсутствии представлений о научной работе.
Так что хорошая статья!
У меня был повод «обидеться» на индекс Хирша. Даже опубликовал в одном Festschrift’е заметку «Проделки с индексом Хирша». Мне доказывать значимость своего вклада не приходится (возраст). Более 650 публикаций в том числе многие в престижных изданиях мира (по моей специальности), четыре десятка книг (в том числе двухтомников) на основных языках. Статьи обо мне в энциклопедиях. А индекс Хирша маленький (2 или 3), чем один из моих противников и воспользовался.
Но, во-первых, ведь моя специализация (археология, культурная антропология, история, филология) в основном не затрагивается той базой, по которой вычисляется индекс Хирша. Он просто здесь пока неприменим. Во-вторых, индекс Хирша вообще оставляет в стороне монографии и их оценку. Он также не учитывает число переводов на другие языки. Я уж не говорю о качестве ссылок: упоминаний Петрика множество, но это еще не говорит о его вкладе в науку.
Очевидно, для чиновников индексы оценки необходимы, и их надо совершенствовать. Но профессионалы хорошо знают, кто есть кто без всяких индексов. Даже студенты знают.
знать то они знают, да только что толку от этого знания?
Речь ведь идет о том, что вопреки этим знаниям, зарплата у них ничтожная потому, что нет министерского, просто бухгалтерского индекса и учета их труда.
Ну почему же этому нужно противится?
Ну как ее платить, чтобы все видели хорошего сотрудника, и зарплата его соответствовала этому видению.
Именно это обсуждаем. Хочется, не хочется, нужно это вводить.
А вот эти штуки «все знают» — не надоели они вам? Неужели не понимаете, что и кто за этим стоит? Шамхалова как раз таки «все знали».
Да! Для каждой области индексы свои и т.п. и т.д. Все это уже обсуждали 1000 раз.
Но не быть их совсем не может. Тогда так и будем в академики самых отстойных брать, которых «все знают», неизвестно почему..
еще короче — коллеги знают о хорошем сотруднике,
А БУХГАЛТЕР — НЕТ! Так дайте ему знать цифрой! Не упрямьтесь!
а то, что у вас Хирш низкий, это сигнал к тому, чтобы придумать иной показатель.
Для этого нужно предлагать, а не критиковать.
Ведь в каких-то областях Хирш работает.
Не совсем понимаю возмущение Начинающего Алкоголика. Я ведь ни словом не возражаю против введения индексов оценки. Я говорю лишь о необходимости расширить критерий оценки. И Хирша я отнюдь не отвергаю, я говорю лишь о его ограниченности. А вот этот пассаж и вовсе мимо цели:
-«А вот эти штуки «все знают» — не надоели они вам? Неужели не понимаете, что и кто за этим стоит? Шамхалова как раз таки «все знали».
Уважаемый Начинающий! Уверен, что Шамхалова все знали не как ученого, а как дельца на этой ниве, у которого можно добыть кандидатский диплом. И только. Какие его теории, аргументы, открытия, достижения в науке? Их нет, их не знал и не мог знать никто.
Есть такая штука — гамбургский счет. По-простому — имя в науке. Когда у человека есть имя, когда люди сбегаются на его доклады, когда за его статьи соревнуются журналы, а молодежь записывается к нему в ученики, — ему не нужен никакой индекс. Даже бухгалтера как-то обходятся. И это не зависит от титулов.
Все археологи знают Вадима Б. Он лучший специалист по бронзовому веку Восточной Европы, величина европейского масштаба. Так получилось, что он не доктор и даже не кандидат наук. Вообще-то он защищал кандидатскую диссертацию, и совет единогласно присудил ему докторскую. Но ВАК не утвердил: рано, слишком молод. И в результате он не получил никакой. Вадим обиделся и более не стал подавать на защиту. Так и проходил всю жизнь (сейчас он в пенсионом возрасте). Ученики его доктора, а он нет. Но имя Б. — это марка высоча
продолжаю: высочайшего качества. Перед нами же его труды, его классификации, его системы знания, его идеи. Их развивают многие. Не его оценивают по индексу, а индексы проверяют на соответствие значению этой личности.