
Дэвид Таулес (David J. Thouless), Майкл Костерлиц (J. Michael Kosterlitz) и Дункан Халдейн (F. Duncan M. Haldane) — очень известные физики-теоретики классической школы, т. е. это люди именно что развивающие науку, а не делающие бизнес на науке, как это становится всё более привычно наблюдать в последнее время. Все они специалисты по квантовой теории конденсированного состояния вещества — одной из самых малоизвестных широкой публике областей физики.
Малоизвестна она потому, что она весьма сложна для популярного изложения, т. е. «в два притопа» никак не получится. Даже квантовую механику одного электрона довольно сложно объяснить тем, кто не изучал этой науки всерьез, но хотел бы «быстро узнать самое главное» и недоумевает, почему это не удается объяснить за десять минут. Здесь же речь идет о квантовой механике систем с очень большим числом частиц (например, 1010 или даже 1020) .
Последние лет примерно шестьдесят многие очень сильные физики-теоретики занимались именно таким классом задач и много чего интересного придумали (первые результаты в этой области были получены Львом Ландау в 1950-х годах). Однако сведения об этих достижениях становятся известны в лучшем случае 5–10% выпускников ведущих физических факультетов лучших профильных вузов.
Примерно понятно, почему Таулес выделен среди этих троих (он получает половину премии, а Костерлиц и Халдейн делят другую половину). Дело в том, что Таулесу принадлежат важнейшие результаты по крайней мере по двум различным фундаментальным задачам.
Фазовые переходы в двумерных системах
Одна из них — и это их совместный с Костерлицем результат 1973–1974 годов — очень необычная на тот момент теория фазового перехода в двумерных системах (применимая и к плавлению двумерного кристалла, и к разрушению сверхпроводимости или сверхтекучести в тонких пленках, и еще много к чему подобному).
В отличие от ранее существовавших теорий фазовых переходов, в теории Костерлица и Таулеса основную роль играют топологические дефекты той структуры, которая реализуется в упорядоченном состоянии вещества. Например, для двумерного кристалла такой дефект — дислокация. А для тонкой пленки сверхтекучей жидкости (или сверхпроводника), а также двумерного ферромагнетика соответствующий дефект — квантованный вихрь.
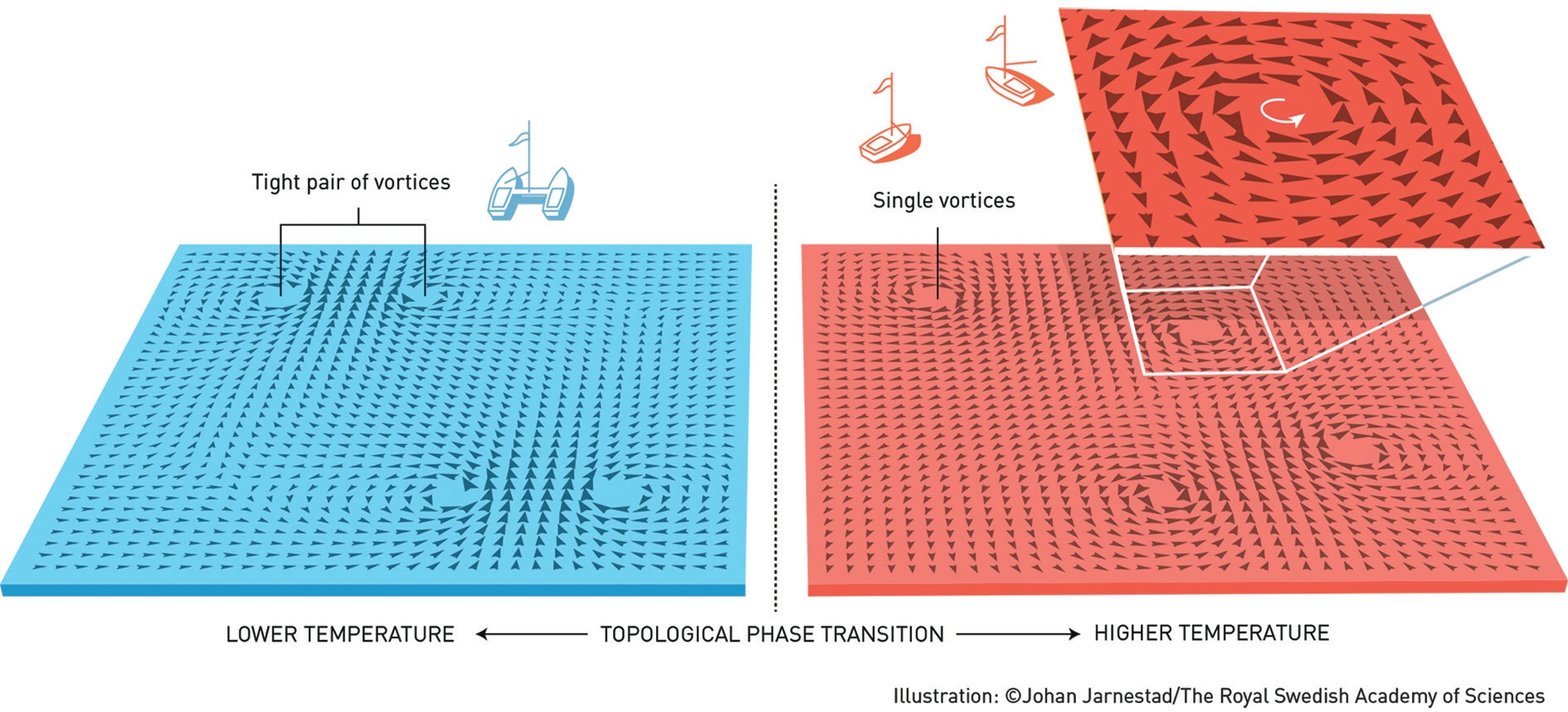
Во всех случаях топологический дефект определяется через сингулярность в распределении «параметра порядка», т. е. величины, характеризующей отличие упорядоченной фазы вещества от неупорядоченной. Наиболее наглядный вид такой дефект имеет в случае двумерного ферромагнетика, у которого намагниченность лежит преимущественно в одной плоскости (определим ее как плоскость XY).
Местоположение вихря — это такая точка, что если обойти вокруг нее по целой окружности и всё время следить за направлением намагниченности M, то окажется, что вектор M тоже описал полную окружность на плоскости XY. Топологическим этот объект называется потому, что осуществляет нетривиальное отображение окружности в реальном пространстве на окружность, отвечающую фазе вектора параметра порядка M.
Существенно также, что результат обхода вокруг этой сингулярной точки не зависит от того, по какой именно окружности мы ее обходили (и вообще это может быть не правильная окружность, а любая замкнутая траектория, имеющая нашу особую точку внутри себя).
Оказывается, именно свойства таких «топологических дефектов», и в частности зависимость энергии пары дефектов противоположного «знака» от расстояния, определяет границу устойчивости двумерной упорядоченной фазы. Реальных физических ситуаций, где реализуются предсказания теории Майкла Костерлица и Дэвида Таулеса, очень много. И это важно, потому что большинство новых открытий в физике конденсированного состояния последних десятилетий относится именно к низкоразмерным системам (тонким пленкам или проволокам).
Стоит еще вспомнить, что работу, по существу очень близкую к работе Костерлица и Таулеса, независимо сделал в 1971 году выдающийся российский физик-теоретик Вадим Березинский. Его имя отлично известно специалистам и упоминается в соответствующих статьях вместе с Костерлицем и Таулесом. Но претендентом на Нобелевскую премию он сейчас никак быть не мог, ибо, увы, умер более 30 лет назад.
Квантовый эффект Холла
Другая фундаментальная работа Таулеса, выполненная в соавторстве с Махито Комото (Mahito Kohmoto), Питером Найтингейлом (Peter Nightingale) и Марселем ден Нийсом (Marcel den Nijs), связана с теорией квантового эффекта Холла, где также были использованы топологические соображения.
Эффект Холла — это появление напряжения Vy в направлении, перпендикулярном направлению протекания тока Ix, когда к проводнику приложено магнитное поле в направлении z. Соответственно, холловская проводимость определяется как sH = Ix / V y. Квантовый эффект Холла был обнаружен в начале 1980-х годов при исследования полупроводниковых гетероструктур, помещенных в сильное магнитное поле, и состоит он в том, что холлов-ская проводимость принимает набор лишь целочисленных значений sH = n e2/h (здесь e — заряд электрона, h — постоянная Планка, а n — целое число).
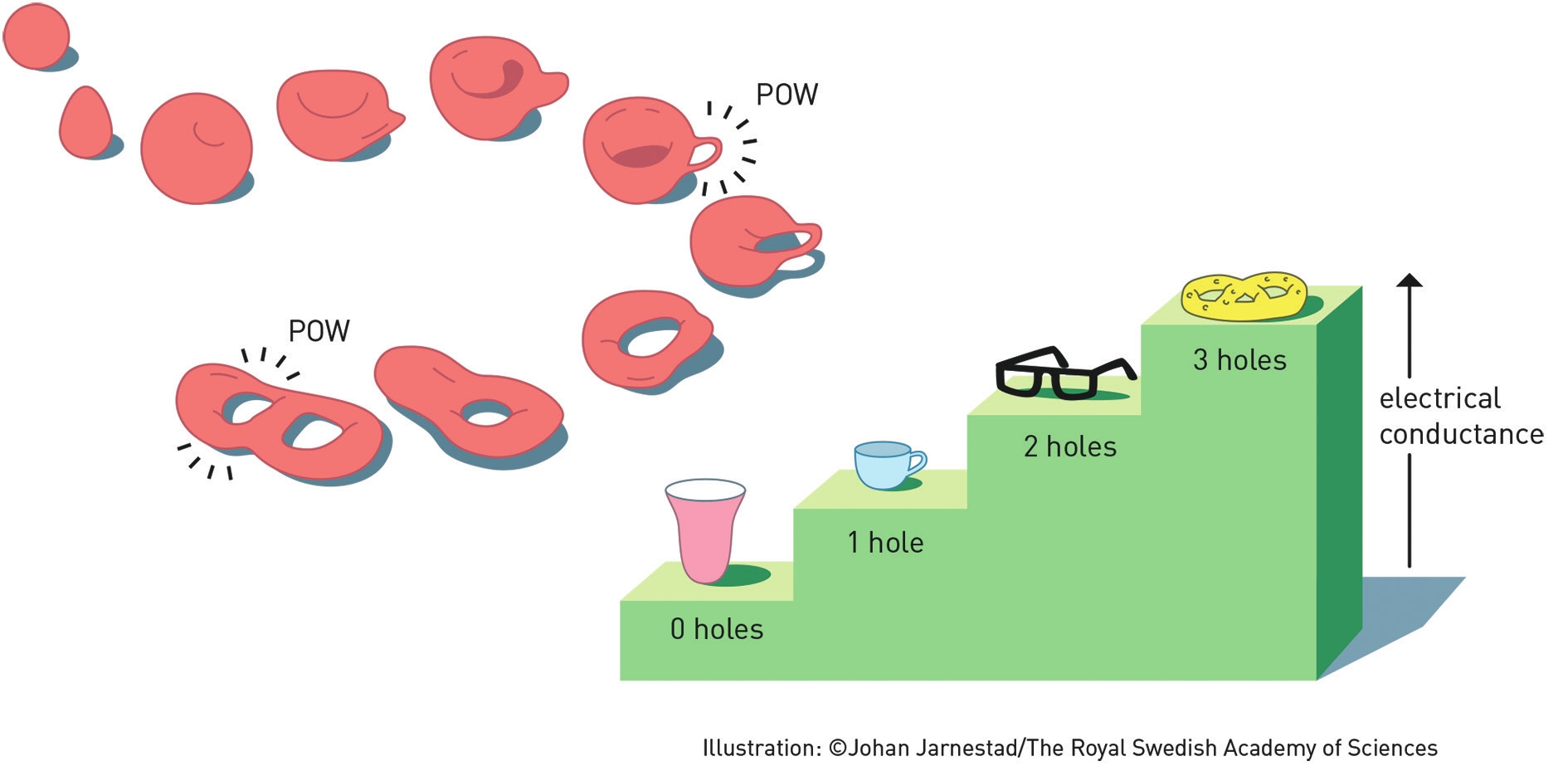
Точность квантования холловской проводимости при низких температурах очень велика, порядка 10-8 в относительных единицах, и поэтому квантовый эффект Холла оказался важным для метрологических приложений. В работе Таулеса и соавторов речь шла о доказательстве связи между холловской проводимостью и степенью отображения двумерного тора (т.е. квадрата, противоположные стороны которого попарно отождествлены между собой) на другой подобный тор.
Целое число n в величине sH оказалось, с математической точки зрения, именно степенью отображения тора на тор. Тем самым было показано, как можно понимать целочисленность значений sH в единицах e2/h.
Экспериментальное обнаружение (за что получил Нобелевскую премию 1985 года германский физик Клаус фон Клитцинг (Klaus von Klitzing)) и затем построение теории квантового эффекта Холла — одно из важнейших достижений физики конца XX века.
Одномерные квантовые магнетики
Один из важнейших результатов Дункана Халдейна — теория одномерных квантовых магнетиков, объясняющая, почему их свойства принципиально различны в случаях, когда спин отдельного атома целый или же полуцелый.
Здесь надо, во-первых, объяснить, что такое одномерные магнетики. Конечно, почти все физические тела трехмерны. Однако бывает так, что с точки зрения какого-то конкретного эффекта, который мы в данный момент изучаем, наша система состоит из набора не связанных между собой одномерных цепочек.
Так бывает, если магнитные атомы располагаются в виде цепочек и магнитное взаимодействие между спинами разных цепочек очень слабое. Тогда хорошее приближение к задаче — считать, что мы имеем дело с набором независимых друг от друга цепочек. Свойства системы квантовых спинов ½ (как у электрона или протона) сильно отличаются от свойств аналогичной системы, сделанной из классических векторов — «стрелочек».
Обычно все квантовые эффекты пропадают, если изучать систему с достаточно большим спином S >> 1. Халдейн показал, что для большого класса одномерных магнитных цепочек это не так: имеется принципиальное различие спектров возбуждений между цепочками со спинами S = n и S = n + ½, даже если целое число n очень велико.
Для полуцелых спинов спектр возбуждений всегда начинается с нуля, т. е. есть элементарные возбуждения сколь угодно низкой энергии, в то время как в случае целых спинов в спектре всегда имеется ненулевой порог. В этой работе также было использовано понятие, имеющее отношение к топологии. Речь шла, как и в работе Костерлица и Таулеса, о роли «топологических дефектов», однако теперь это дефекты более сложные: они отображают двумерную сферу на саму себя.
Вклад таких дефектов оказывается пропорциональным exp (2π i S) = (–1)2S , т.е. равен единице для целых значений спинов S, но (–1) для полуцелых S. Дункану Халдейну удалось установить связь между знаком вклада от топологического дефекта и свойствами спектров возбуждений длинных спиновых цепочек. Как и в более простом случае, исследованном Костерлицем и Таулесом, эта работа показала важность (и возможность!) учета редких больших флуктуаций квантовых полей для выяснения самых фундаментальных вопросов, связанных с физикой низкоразмерных систем.
Михаил Фейгельман,
докт. физ.-мат. наук, зам. директора Института теоретической физики им. Ландау РАН



Что-то Фейгельман «уже не тот».
Березинский не просто сделал «работу, по существу очень близкую к работе Костерлица и Таулеса», а получил все основные результаты, которые и были отмечены нобелеским комитетом. К. и Т. переписали работу Березинского, возможно более понятными словами.
В такой ситуации корректно было бы вообще не премировать товарищей К. и Т., ибо первооткрывателя и внесшего решающий вклад уже нет в живых (к огромному сожалению).
Но это уже отнюдь не первый случай ангажированных и нарушающих этику и здравый смысл решений нобелевского комитета.
Первооткрыватель Лев Давидович Ландау выпустил свои работы в 50-х годах задолго до Березинского. И он лауреат Нобелевской Премии. А в чем Ваша претензия к Нобелевкому Комитету?
Мерзкий гнилой тролль, твоя намеренная дезинформация не останется опровергнутой: первооткрыватель Л.Д. Ландау был удостоин премии за свои оригинальные результаты, в которых не было даже намека на оригинальные результаты, полученные впоследствии первооткрывателем Березинским.
То, что ты хочешь внушить: «у вас уже есть например Ландау среди лауреатов, вот и радуйтесь.»
Слив засчитан спасибо. Вот она «культура» научной дискуссии по-путински личные оскорбления из уголовной подворотни вместо фактов.
Про твою «культуру» не-научной не-дискуссии я тебе уже всё написал.
Понятно, что факты ты воспринимаешь как личные оскорбления.
так а что такое дислокация для двумерного кристалла? Возьмем, например плотноупакованные твердые диски на плоскости. Затем уменьшим концентрацию, где эта дислокация появляется?
Мне кажется текст написан очень небрежно и очень грешит не точностями. Безусловно проблема актуальна, не только для физики конденсированного состояния, но и для квантовой теории поля. Понятно, нужно автору дать больше места для текста и, может тогда, текст был бы интересен для многих читателей.