Виктор Анатольевич Васильев родился в 1956 году в Москве. Окончил мехмат МГУ в 1978 году, аспирантуру МГУ (под руководством В. И.Арнольда) в 1981 году. С 1995 года работает в МИАН, главный научный сотрудник Отдела геометрии и топологии; с 2008 года — профессор факультета математики НИУ ВШЭ. Виктор Анатольевич с 2010 года возглавляет Московское математическое общество; член экспертной комиссии РСОШ по математике, академик РАН. Сфера интересов: топология, теория особенностей, интегральная геометрия, комбинаторика, теория сложности вычислений.
Про политику
— Мы можем разговаривать про две вещи: математику и политику. Поскольку я в математике ничего не понимаю, наверное, придется про политику.
— Про политику я ничего не понимаю.
— Это хорошо. Я тоже, поэтому мы в равном положении. Когда мы в этой же комнате беседовали с Мишей Цфасманом, он в конце сказал, что темперамент ему не позволяет делать какие-то сильные политические жесты. А Вам позволяет?
— Не знаю. Разве я что-то делал такое? Особенно ничего.
— Те, кто делал что-то особенное, уже профессиональные политики. Если их не учитывать, то оказывается, что Вы делали сильно больше других. Скажем, Ваша фотография перед автозаком — вполне фольклорная. Это не тривиальное гуляние по Москве, когда ходили десятками тысяч, это было перед судом, куда приходили уже совершенно сознательно и конкретно. Я пытаюсь правильно сформулировать вопрос и не очень могу, что-то как у Мольера: «Кой черт понес его на эти галеры?» Что Вас мотивировало?
— Я не знаю. Как-то стыдно было, да.
— «Да» — что?
— Взять и не пойти.
— А как Вы узнали? Про суд, про место?
— Из «Фейсбука».
— У меня была аналогичная ситуация: уже когда судили Вас, то тоже было стыдно не пойти — такая цепная реакция. Вам штраф потом присудили?
— Присудили.
— Вы его заплатили?
— Заплатил.
— Сами?
— Я заплатил, конечно, из своих, но, если посчитать людей (их было много), которые мне предлагали скинуться заплатить, я бы мог сделать очень хороший бизнес. Но все-таки я человек достаточно обеспеченный по нашим временам.
Про учебники
— Вы довольно долго были председателем академической комиссии по школьным учебникам.
— Да.
— Что, я подозреваю, дело менее яркое, но не менее захватывающее, чем демонстрации.
— Да, там были сюжеты. Люди ходили с адвокатами…
— На заседания комиссии или потом?
— Они в основном Козлова (В. В. Козлов, вице-президент РАН. — Прим. ред.) пугали адвокатами.
— Козлов был председателем комиссии по всем учебникам, а Вы — по математике?
— Да. Мы, представители всех дисциплин, собирались, докладывали свои дела, потом дела как-то утверждались, и с этим что-то происходило.
— Удавалось делать что-то разумное?
— Да.
— То есть это был хороший инструмент?
— Да, хотя намного меньше того, чего хотелось бы. Было какое-то количество авторов, про которых сразу понятно, что они ничего хорошего никогда написать не смогут. Их удавалось задержать на три-четыре года. Но потом это всё равно продавливалось, потому что наши полномочия заключались только в математических ошибках. Я представляю очередной список, они их исправляют, и рано или поздно всё заканчивается. А то, что человек не понимает, для чего это всё нужно и как всё связано, нам говорить запрещалось.
— Потому что вы не педагоги, а математики.
— Да. Была отдельная педагогическая комиссия, которая потом, когда произошла революция, зарубила всё.
— Революция?
— Вышел новый регламент экспертизы, пошла новая политика, когда стали рубить учебники, например, по причине непатриотичности. Какой-то не наш Винни-Пух в задачах…
— Что не отменяет математических ошибок. Это мог быть дополнительный фильтр у педагогов, но он не влиял на деятельность комиссии.
— Тогда зарубили хорошие математические учебники. Произошла глобальная подковерная революция, когда главный наш почти что монополист — издательство «Просвещение» — приобрел нового начальника по имени Аркадий Ротенберг.
— Я помню, в Общественном совете Минобрнауки в это время тоже были большие обсуждения.
— Так совпало, что их конкурентов после этого стали выносить уже без стеснения.
— Что же все-таки случилось с академической комиссией? Или ее просто перестали спрашивать?
— Я тогда резко взбрыкнул, в частности по поводу нового регламента экспертизы (см. http://atlmrf.livejournal.com/11075.html. —Прим. ред.). Я демонстративно ушел, ко мне уже даже не подходили по этому делу, и всё заглохло.
— То есть поставлен эксперимент, который показал, что комиссия была работоспособна только благодаря одному человеку.
— Довольно долго всё работало. Даже плохие учебники, которые в конце концов проходили, становились лучше. Одно дело — учебник изначально, другое дело, когда мне удавалось исправить в нем, допустим, 360 ошибок за четыре года.
— Сколько народу реально работало в комиссии, то есть действительно тратили заметное время?
— У меня в комиссии таких и не было. Я был один, но просил разных людей помочь. Сначала за смешные деньги, потом, когда наверху убедились, что от нашей деятельности есть прок, стали платить деньги, которыми стало можно кого-то соблазнять.
— Фактически Вы координировали рецензентов?
— Я на самом деле такой гениальный менеджер, так хорошо могу организовывать людей, что потом большую часть приходится самому переделывать. Довольно долго я работал в таком режиме. Было несколько человек, которые работали более-менее хорошо. Под самый конец, последние два года, у меня случилась удача: я связался с надежными и добросовестными людьми из Дубны, связанными с ОИЯИ. Жизнь там ухудшается, но все-таки цены областные. Им платили московские деньги, и они оказались очень заинтересованы. Работа пошла, я разгрузился. Но я как-то подсчитал, что за это время сам прочитал 250 учебников.
— «Прочитал» надо понимать как «внимательно прочитал»?
— Внимательно прочитал, в частности прорешал задачи. Некоторые не до конца, а до сотой ошибки (или до шестидесятой, когда был полный завал с учебниками).
— Есть такой иезуитский способ: каждый раз до шестидесятой ошибки дочитывать, а про все остальные ничего не говорить, чтобы побольше итераций было.
— У меня просто сил не было дальше читать. Как-то раз за лето надо было прочитать тридцать три учебника. То есть их дали шестьдесят девять, тридцать шесть я раскидал по рецензентам, а тридцать три не раскидал. У меня было на учебник три дня. Вот тогда я на кофеин подсел и никак не могу от этого избавиться.
— При такой работе можно подсесть и посерьезнее. Опять тот же вопрос: что за мотивировка, чтобы этим заниматься?
— У меня дети были в школе в это время, и я заметил, что с наибольшим рвением я относился к учебникам того класса, в котором они будут учиться на следующий год. Но не только. На самом деле такая контрольная деятельность вредна для психики. Выслеживать кого-то, ловить, ущемлять… Приходилось как-то себя мотивировать.
— Мотивировать, чтобы заниматься, или, наоборот, чтобы не превратиться в совсем жандарма и не радоваться на каждый новый ляп?
— Сначала я мотивировал ловить, поймать, не допустить. Потом начал стараться, чтобы это не переросло в доминанту. Но все-таки заставлять себя таким делом заниматься довольно трудно. Я строил себе какие-то картинки, воображал поле, заполненное детьми, в первых рядах даже какие-то лица прорисовывал. И вот я перед ними стою и защищаю их от мерзости, которая на них наступает. В общем, это был такой опыт… Ой, я разоткровенничался.
— Хорошо-хорошо.
— Противно было, как-то надо было себя заставлять.
— Вот сейчас мы члены президиума ВАК: я — по наукам о жизни, Вы — по естественным наукам, а встречаемся на заседаниях по гуманитарным наукам. Зачем Вы туда ходите?
— Вам помогать. Лично Вам и Диссернету.
— Теперь Вы вместо детей представляете себе одинокого сражающегося меня?
— Не Вас одинокого. Вы, одиноко сражающийся за нашу науку; бедные студенты, которых эти придурки будут потом учить. Ну как же Вам не помочь?
Про занятия математикой
— Попробую спросить про математику. Есть ли разница в мотивировках для занятий математикой сейчас, тридцать лет назад и сто лет назад? Тридцать лет назад Вы уже по собственному опыту знаете, а сто лет назад — предположительно.
— Я сейчас другой человек. Тридцать лет назад у меня с мотивировками было гораздо проще: все кругом занимаются, компания хорошая.
— Мало ли хороших компаний?
— Ну, я родился в такой семье, мне было внушено, что если потратишь жизнь на математику, то ты ее не зря прожил. Не зря потратить жизнь — это, собственно, главная мотивировка для людей.
— Сейчас мотивировка изменилась?
— В общем, нет. Сейчас, конечно, возможностей больше, но для меня всё равно лучший способ потратить жизнь — это заниматься математикой и ее преподаванием, потому что мне сильно перестраиваться на что-то другое уже поздно. А это дело хорошее, дети такие хорошие у нас растут, просто замечательные.
— А разговоры про то, что студент пошел не тот?
— Понимаете, мы у себя в Вышке (на факультете математики Высшей школы экономики. — Прим. ред.) снимаем сливки. Те, кто попадает к нам, они очень хорошие. Может, даже получше, чем когда-то были. Некоторые просто совершенно замечательные ребята.
— За счет улучшения процедуры снятия сливок, или что-то поколенческое? Или просто человечество становится умнее?
— Я не знаю. Конечно, наше факультетское начальство разумное, оно и сливки разумно снимает.
— Нет ощущения, что все умные дети уехали?
— Очень много умных детей уехало, но не все. Многие остаются, кто-то уезжает-приезжает. У нас полфакультета преподавателей — это люди, которые уехали и вернулись. «Полфакультета» — это, конечно, не строго. Я не знаю, сколько в процентах, но очень много.
— А у них какая мотивировка, чтобы заниматься математикой?
— Ой, очень сложно. Тут жизнь идет.
— То есть в значительной степени мотивировка тоже социально-психологическая? У меня-то ощущение, что чисто генетическая: в каждом поколении есть процент людей, которые ничего другого не могут.
— Да, конечно. Среди самых талантливых детей видно, что это дети от бога.
— Откуда они приходят?
— По-разному. Довольно много сильных детей приходит из СУНЦа.
— То есть Колмогоровский интернат или московские математические школы. Бывают совсем самородки, которые в лаптях приходят неизвестно откуда? В биологии так бывает. Я видел таких детей, которые вообще непонятно откуда взялись.
— Нет, совсем в лаптях если бывают, то очень редко. В основном через интернат или сильные региональные школы. У нас есть несколько таких рассадников.
— От чего это зависит? Появляется хороший учитель?
— Да.
— Получается чистое везение: если человек живет в городе, где есть хороший учитель, то у него есть шанс; а если в городе, где нет хорошего учителя, то никто и не узнает. Как у Марка Твена: самый гениальный полководец — сапожник, который никогда не воевал, потому что хромал и его не взяли в армию.
— Так и есть, к сожалению. Очень много людей пропадает, судя по статистике.
— Вы говорили, что поздно перестраиваться, слишком много времени уйдет на переобучение. А если пофантазировать? Если вдруг все-таки перестроиться, то что бы было?
— Не знаю.
— Дело не в том, что тяжело перестраиваться, а в том, что не хочется?
— Математика мне подходит еще и по темпераменту, потому что в других областях очень много значит уметь себя поставить, надо быть борцом. А в математике если показал, что умеешь решать задачи, то вот ты уже и умеешь.
— Скорее не решать задачи, а придумывать.
— Ну да, и придумывать. Всего понемножку.
— Я понимаю, что Вы имеете в виду. Чтобы заниматься экспериментальными науками, надо уметь деньги выцыганивать. Гранты писать.
— Между прочим, все 1990-е годы я, опять-таки, как великий менеджер, писал гранты. У меня было некоторое количество групп, на которые я писал заявки, а потом писал отчеты.
Про математику
— Продолжая линию дурацких вопросов: что интересного сейчас происходит в математике? Или про математику нельзя так спрашивать?
— Можно. С одной стороны, есть области, которые быстро растут, в них работает много сильных людей, которые выводят это дело на новый уровень абстракции, связывают с чем-то. Такая область развивается. С другой стороны, время от времени решаются старые классические задачи, причем часто за счет того, что обнаруживается удивительная связь с иной областью математики.
— Например?
— Примерно полгода-год назад украинско-немецкая девочка (Марина Вязовская. — Прим. ред.) решила знаменитую задачу про упаковки шаров, которая стояла много лет. В восьмимерном пространстве некоторая упаковка действительно является оптимальной, совершенно не улучшаемой. Причем решено это было за счет соображений из функционального анализа, теории представлений и теории модулярных форм. Я немножко смотрел: не только ее работа, но и всё, что ей предшествовало, — совершенный восторг.
— Почему именно в восьмимерном?
— Восьмерка здесь вообще священное число. Восьмерка в этой науке появляется очень часто. В теории решеток, то есть периодических структур, есть теорема, что только в размерностях, кратных восьми, бывают решетки с некоторыми исключительными свойствами. И вот про такую решетку в восьмимерном пространстве сразу было видно, что она замечательная, что в соседних размерностях ничего подобного нет. Тогда возникло предположение, что она будет задавать оптимальную упаковку, но доказать это долгое время было невозможно.
— А в соседних размерностях нет ничего интересного, только тривиальные решения? Или, наоборот, нет никакого решения?
— Вообще непонятно, что делать. Там хаос, нет приличных гипотез. Есть экспериментальные факты, есть какие-то простые оценки, которые с двух сторон, но далеки друг от друга. А здесь оценки совпали.
— Есть банальные примеры таких задач: теорема Ферма и гипотеза Пуанкаре. А менее банальные?
— Ситуаций, чтобы задача долго стояла и потом чудесным образом решалась, я в последнее время, пожалуй, не припомню. Другой пример на ту же тему: долго добивали задачу о размерности три. Там другое: добит ответ, совершенно очевидный, при помощи работы десятка людей, с компьютерными экспериментами. Они оценивали-оценивали какие-то хвосты и все-таки оценили.
— Это кеплеровские укладки, гексагональная и кубическая?
— Да.
— Про них тоже долго не было доказано, что они оптимальные?
— Да. Дожали сравнительно недавно. Это пример силового решения проблемы, когда жали-жали традиционными методами и таки дожали. Но это очень далеко от того, чем я занимаюсь. Где я занимаюсь, даже не знаю, чем Вас порадовать.
— А чем Вы занимаетесь?
— Я в последнее время занимаюсь неизвестно чем. Потому что я и раньше занимался много чем, а сейчас мои последние работы строятся по одному образцу, довольно дурному. Ко мне обращаются из какого-нибудь журнала, что вот, мол, мы делаем юбилейный или памятный номер; не можете ли Вы нам что-нибудь написать. И, как правило, бывает понятно, на какую примерно тему. Я начинаю вспоминать, что раньше делал в данном направлении. В конце концов вспоминаю,
что, когда я этим занимался, была у меня мыслишка, мол, что же они все не понимают такой-то вещи. И раз просят, то можно про это написать. Время от времени решаются задачи, на которые я тогда забил.
Мой любимый результат: ему уже, правда, три года, его я мечтал доделать 25 лет. У меня был некоторый прорыв в 1987 году, и потом я долго пытался дальше что-то сделать. Задача в двумерном случае восходит к Ньютону. Про нее писали разные работы, но все в двумерном случае. Как раз в 1987-м праздновали 300-летие главной книги Ньютона, Арнольд стал по этому поводу Ньютона изучать, наткнулся на эту задачу и поставил ее так: а нельзя ли подобное сделать в старших размерностях. Он поставил задачу на семинаре и еще попросил почему-то именно меня это сделать. Через какое-то время получилось пробить это в каких-то частных случаях, например в выпуклом случае.
— Что все-таки за задача?
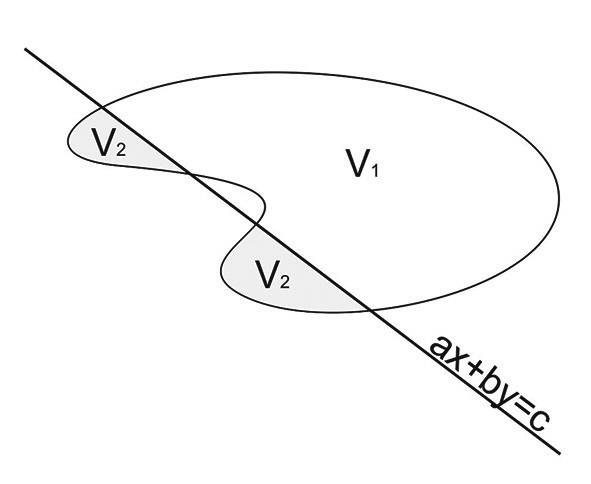
— Из интегральной геометрии. У нас в сколько-то мерном пространстве — у Ньютона в двумерном — есть тело, ограниченная область пространства с гладкой границей. Тогда эта область определяет такую функцию на множестве всех гиперплоскостей в этом пространстве: объем, который гиперплоскость отсекает от тела в ту или другую сторону.
— То есть в двумерном случае мы имеем плоскую фигуру, рассматриваем все прямые, которые ее пересекают, и соотношение площадей с одной и с другой стороны?
— Не соотношение, а берем одну и другую площадь. Получается двузначная функция. Что это будет за функция? Будет ли она алгебраическая? Знаменитая теорема Ньютона состоит в том, что в двумерном случае функция не может быть алгебраической: не существует нетривиального полинома, который обращается в ноль, когда в него подставлены параметры гиперплоскости и отсеченные объемы.
— Надеюсь, в двумерном случае я смогу понять.
— a, b, c — это коэффициенты уравнения прямой, а еще есть V — площадь отсеченной части.
— V1 и V2.
— Да (рис. 1). Функция V (a, b, c) была бы алгебраической, если бы существовал такой многочлен P (a, b, c, V), который не равен тождественно 0, но обращается в 0 каждый раз, когда V является одной из площадей, отсеченных прямой с коэффициентами a, b, c. Но такого многочлена не существует. Вот такая теорема.
— Ньютон умел это доказывать?
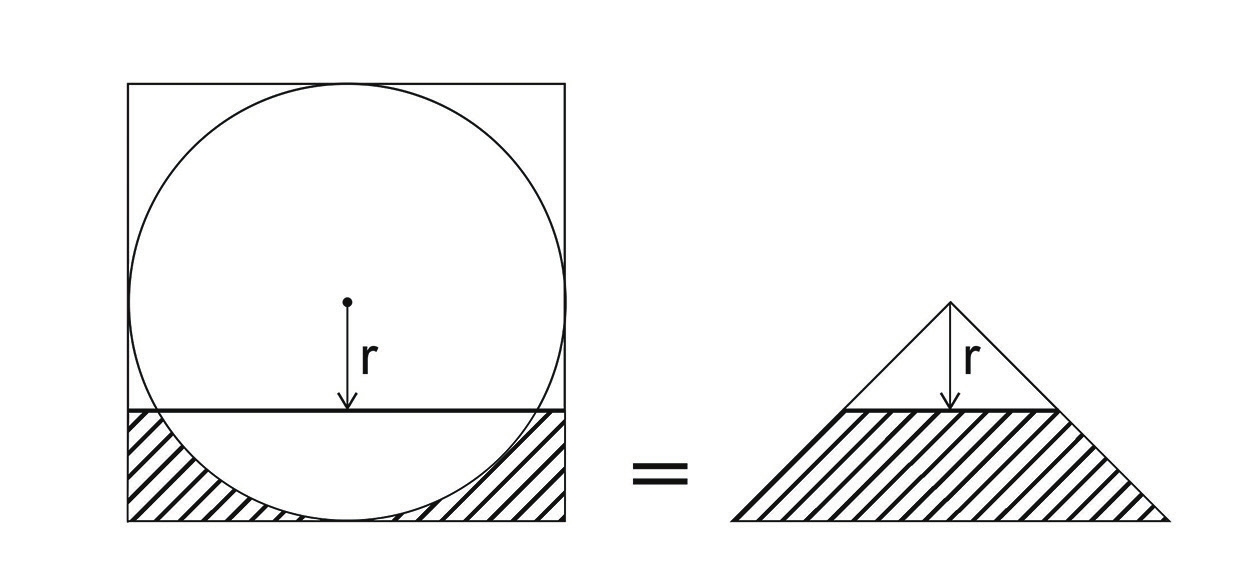
— Да, по тогдашним стандартам строгости он научился доказывать в двумерном случае. Интересно, что Архимед немножко раньше доказал, что в трехмерном-то случае функция будет алгебраической, например, для сферы. А в двумерном случае алгебраичности нет.
— Даже для окружности?
— Ни для чего нет. Не существует такого тела, чтобы это было алгебраично. А Архимед доказал, что для сферы в трехмерном пространстве, тем самым для эллипсоида — немножко поковырявшись, легко понять, что для любого эллипсоида в любом нечетномерном пространстве, — алгебраичность будет.
— В каких терминах Архимед формулировал? Он же не знал слова «многочлен».
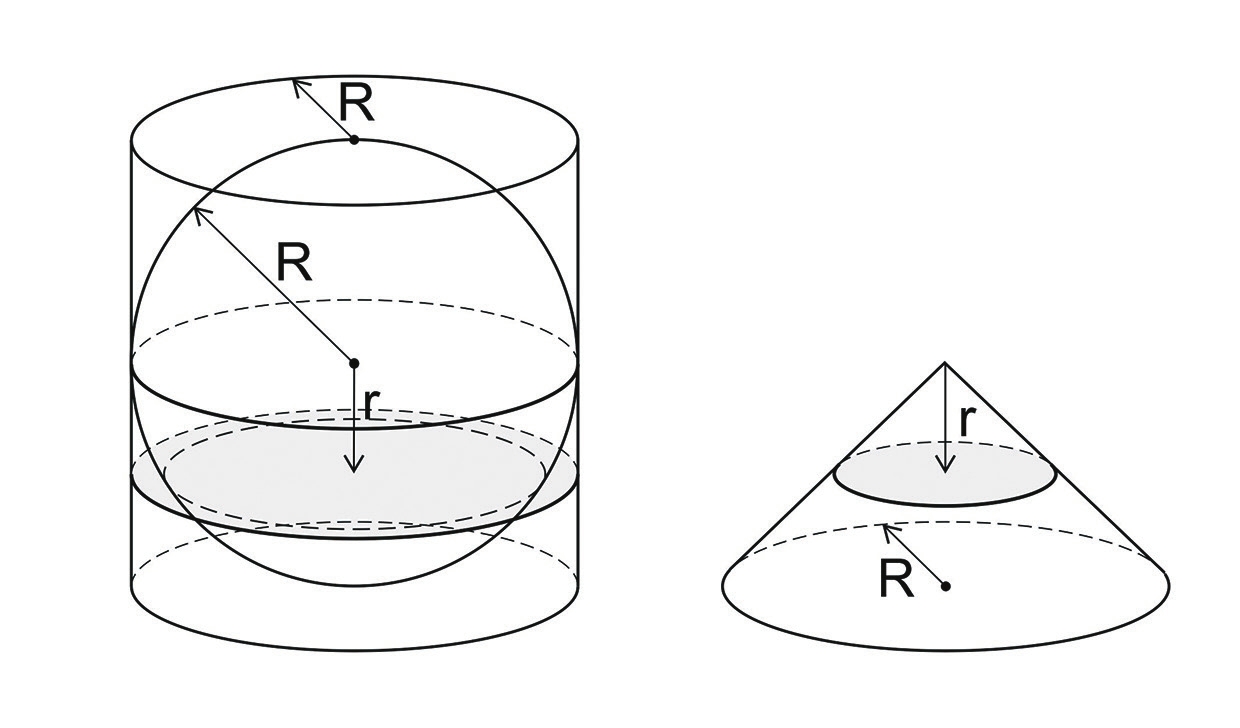
— Но он явно вычислил. Теорема Архимеда состоит вот в чем. Мы берем сферу и отсекаем от нее луночку плоскостью, которая проходит на расстоянии r от центра. Архимед вычислил объем этой луночки. Надо взять эту сферу, погрузить в цилиндр, а рядом еще поставить конус с таким же основанием, как у цилиндра (рис. 2).
— То есть фактически два радиуса.
— Тогда утверждается, что объем части цилиндра, лежащей под плоскостью, равен сумме объема луночки и усеченного конуса.
— А высота конуса?
— Высота конуса — R (радиус сферы), основание — 2R.
— То есть теорема состоит в том, что дополнение к лунке в этой шайбе равно объему усеченного конуса.
— Да.
— И тем самым полином понятно какой.
— Да, расстояние до центра алгебраически выражается через уравнение плоскости.
Так вот, уютный случай был для выпуклых тел, а теперь я доказал и для невыпуклых, и всё это методом выхода в комплексную область. Что произошло со времен Ньютона — люди научились выходить в комплексную область. И теперь кто попало может доказывать такие теоремы. В 1987– 1988 годах у меня получилось для выпуклых, а потом я хотел доделать это для произвольных тел в четно-мерном пространстве. Я несколько раз брался, а в 2013 году в некоторый момент у меня раз — и всё сложилось. Бывают такие моменты. Я до сих не перестаю радоваться на результат. Да, забавно, что последний гвоздь в доказательстве тоже из теории решеток.
— Сейчас это доказано в четномерном случае для всех, а в нечетномерном — неверно, потому что есть контрпримеры?
— Да. В нечетномерном случае есть задача доказать, что алгебраичность имеется только для эллипсоидов. Тут тоже у меня тогда были какие-то продвижения. Но вот так, чтобы всё сложилось и доказалось, что, кроме эллипсоидов, ничего нет, не получается.
Всё интервью с «Математических прогулок» можно прочитать на:
www.skoltech.ru/mathwalks/
http://iitp.ru/ru/press_center/walks
Виктор Васильев
Беседовал Михаил Гельфанд
Фото М. Ефимовой
Рисунки Е. Гнучих по эскизам В. Васильева


Примерно полгода-год назад украинско-немецкая девочка (Марина Вязовская. — Прим. ред.) решила знаменитую задачу про упаковки шаров, которая стояла много лет.
——————-
«Девочке» уже 32 года.