Нетранзитивность — кладезь для изобретателей

В статье Натальи Резник «Камень, ножницы, бумага» [1] описаны многочисленные забавные — с человеческой точки зрения — взаимодействия самцов в борьбе за самок. У самых разных видов (ящериц, жуков и других) наблюдается сходный сценарий: есть самцы-агрессоры, вторгающиеся на чужие территории и отбивающие самок у тамошних обороняющихся самцов, и есть «тихушники», мимикрирующие под самок, — они не распознаются агрессорами и успешно делают свое черное дело. Зато «тихушников» успешно вычисляют обороняющиеся самцы. Этими очень понятными примерами дело не ограничивается — вопрос ставится значительно шире. Принцип взаимодействий «камень, ножницы, бумага» рассматривается в биологии как один из универсальных, поддерживающий биоразнообразие на самых разных уровнях. В журналах Science, Nature публикуются статьи со словами «камень, ножницы, бумага» в заголовках или списке ключевых слов. В этих текстах представлены живые примеры типа приведенных выше и предлагаются всё более продвинутые математические модели для описания, например, пространственно-временных распределений разных представителей животного и растительного мира (обзор дан в [2]).

Этот спектр явлений получил название нетранзитивной конкуренции — название происходит от логико-математического понятия «нетранзитивность» («непереходность»). Здесь превосходство А над В и затем В над С не распространяется на пару А — С: в ней С может доминировать (побеждать, превосходить А).

Интересна динамика развития разных наук. Изначально независимо, а сейчас всё более пересекаясь при обсуждении общего предмета интереса, на тему нетранзитивности превосходства вышли представители образцового по строгости типа мышления. Это математики — специалисты по теории вероятности, теоретики теории игр и изобретатели логико-математических головоломок. После статей Мартина Гарднера 1970-х годов о нетранзитивных игральных костях (числа на которых подобраны так, что кубик А чаще показывает большее число, чем кубик В, кубик В чаще показывает большее число, чем С, а С чаще показывает большее число, чем А), о нетранзитивных рулетках, наборах игральных карт и так далее пошла широкая волна популяризации темы и ее активного научного исследования [3]. Математическая премия The Carl B. Allendoerfer Award этого года присуждена за статью «Нетранзитивные игральные кости», в которой выявлен еще один важный аспект парадоксальности этих объектов [4, 5]. Что касается популяризации, то в Интернете на слова “nontransitive dice” выпадают десятки видео, где разные люди — от профессоров математики и до школьников — рассказывают о нетранзитивных игральных костях и последствиях нетранзитивности для ошибок научного вывода и реальной жизни. Самая яркая история — о том, как догадливый Билл Гейтс не попал в ловушку с нетранзитивными игральными костями, предложенными ему Уорреном Баффеттом, — фигурирует в самых разных источниках, включая сайт Microsoft [6].

Особый интерес представляет придумывание, изобретение объектов, нетранзитивных по превосходству, то есть таких, что при сравнении по заданному признаку в паре А — В надо выбрать А (как превосходящее В по этому признаку), в паре В — С — выбрать В, а в паре А — С — выбрать С.

Вот некоторые результаты, часть которых получена уже достаточно давно. Разработаны наборы игральных кубиков, в которых при удвоении набора (игроки берут не по одному кубику, а по два одинаковых) меняется направление «битья»: для одиночных кубиков A > B > C > A, а для «спаренных» AA < BB < CC < AA [7]. Также сконструированы наборы кубиков для игры втроем — такие, что, после того как двое игроков выбрали себе по кубику, третий игрок всегда может выбрать выигрышный по отношению к этим двум [7], и набор для игры вчетвером, что намного сложнее [8]. Задача разработки наборов для игры впятером, вшестером и c большим количеством игроков пока, видимо, не решена. Мое предположение: возможно, и здесь (как в ряде некоторых других задач) мы выходим на ключевой вопрос о равенстве классов сложности P—NP. В популярном изложении Лэнса Фортноу, одного из самых известных исследователей в этой области, «P — это класс задач, которые на компьютере решаются относительно быстро. NP — задачи, для которых мы хотим найти оптимальное решение. Равенство P и NP означает, что любую поставленную задачу можно быстро решить. <…> Неравенство P и NP, в свою очередь, означает, что для некоторых задач быстрое решение не найдется никогда» (из книги «Золотой билет. P, NP и границы возможного»). Но обсуждение этого аспекта применительно к нетранзитивных костям мне не встречалось — ни применительно к задаче построения набора костей для N игроков, ни применительно к задаче поиска нетранзитивных цепочек (хотя бы одной или множества цепочек с заданными свойствами) в наборе M костей (например, со случайно сгенерированными числами на гранях). А вот алгоритм генерации таких чисел на кубиках, чтобы те образовывали «простую» нетранзитивную цепочку произвольной длины для игры двух игроков, построен.

При всем интересе к нетранзитивным игральным костям, я занимаюсь изобретением и конструированием объектов, находящихся не в вероятностных, а в детерминистских отношениях непереходности превосходства: начиная с таких геометрических объектов, которые понятны и дошкольнику (в отличие все-таки от нетранзитивных игральных костей), и кончая всё более сложными и контринтуитивными [9]. Помимо забавных моделей, в которых игрушечная птица А кланяется игрушечной птице В (в силу физического взаимодействия их элементов), птица В кланяется птице С, а та — А, здесь есть объекты более парадоксальные и сложные.

Так, создавая зубчатые передачи из двойных шестерен, можно построить такие, в которых двойная шестерня А вращается быстрее В паре А — В, В вращается быстрее С в паре В — С, а С — быстрее А в паре А — С (рис. 1). Иначе говоря, если бы мы играли в игру, в которой выигрывает тот, чья шестерня вращается быстрее, то у игрока, выбирающего вторым, всегда было бы однозначное преимущество; но для того чтобы понять это сразу, надо разбираться в механике.

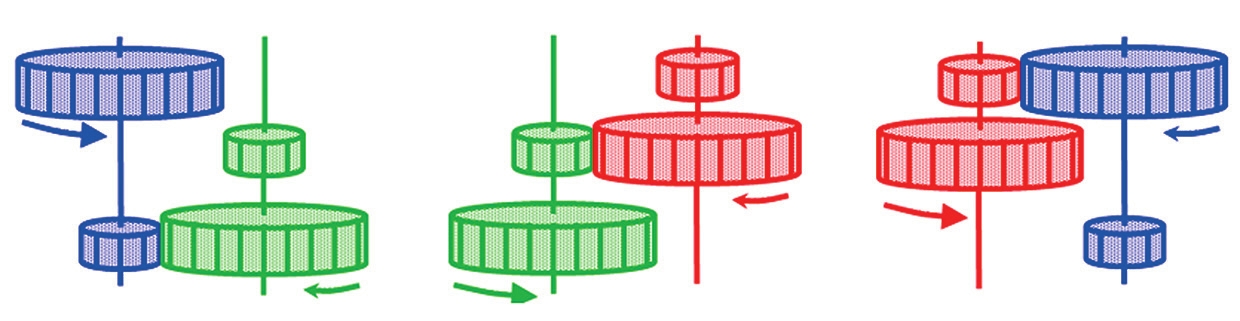
Если же мы будем втыкать оси этих шестерен в расположенные рядом отверстия на вертикальной стенке и закрепим на каждой оси стандартный грузик, то получим кажущийся парадоксальным результат уже в терминах нетранзитивного силового взаимодействия. А именно: при попарных соединениях груз на шестерне А поднимается («пересиливается») грузом на шестерне В, груз на шестерне В — грузом на шестерне С, но груз на шестерне С — грузом на шестерне А (рис. 2). Эта модель может пригодиться для развития представлений учеников в области механики. Аналогично, можно построить нетранзитивные двойные рычаги, где правило рычага и принцип взаимодействия «камень, ножницы, бумага» иллюстрируют друг друга.

Видимо, один из наиболее сложных примеров детерминированной нетранзитивности — нетранзитивные по выигрышности позиции в логических играх на размеченном игровом поле. Это, например, нетранзитивные шахматные позиции: при попарном наложении на одну доску позиция A белых предпочтительнее позиции B черных (при возможности выбора за белых или за черных надо выбрать A), позиция B черных предпочтительнее позиции C белых, позиция C белых предпочтительнее позиции D черных, но позиция D черных предпочтительнее позиции A белых (белые начинают во всех вариантах) (рис. 3). Этот пример сконструирован в демонстрационных целях. Как материал для задачи он лишен шахматного изящества и нарочито прост, даже примитивен, — например, мат может ставиться одним ходом белых. Цель — только показ самой возможности нетранзитивных отношений между шахматными позициями как ранее неизвестного свойства самой шахматной среды (нетранзитивная сила игроков-шахматистов и шахматных программ известна давно).

Пояснение: то, что позиция черных может быть выигрышнее какой-то одной позиции белых и при этом проигрышнее другой, — факт очевидный. Но ранее не была известна возможность нетранзитивного закольцовывания таких позиций, составляющая существенную новизну: ни в каких списках примеров нетранзитивности не удалось обнаружить кольца шахматных позиций. После знакомства с такими позициями у некоторых игроков возникает ощущение очевидности задним числом («ясно, что так можно») — но именно задним.

На основе приведенного на рисунке примера специалист по теории игр А. Ю. Филатов показал, что число нетранзитивных цепочек в шахматах огромно, а сами цепочки могут быть астрономической длины. Также он построил минимальную — и при этом симметричную — цепочку из четырех позиций, где с каждой стороны участвуют только по две фигуры: белые и черные король и пешка [10].

Одно из теоретико-игровых следствий обнаружения нетранзитивных шахматных позиций таково. Получено короткое доказательство важного факта, пусть интуитивно понятного или известного опытным игрокам. В общем случае позиция белых не может быть описана фиксированной количественной оценкой, исчерпывающе характеризующей силу (потенциал) этой позиции — без учета позиции черных. Точно так же позиция черных не может быть описана фиксированной количественной оценкой, исчерпывающе характеризующей силу этой позиции, без учета позиции белых. Сила (потенциал) конкретной позиции белых относительна и определяется ее взаимодействием с конкретной позицией черных, и наоборот.

Это очевидно? Рассмотрим модельный пример. К опытному шахматисту приходит талантливый в шахматах и математике ребенок и говорит: «Я разработал формулу, которая позволяет оценивать по отдельности позицию белых и позицию черных и приписывать им однозначную, фиксированную количественную оценку, а затем сравнивать эти позиции — уже просто как числа, какое больше: у белых или у черных». Вместо ответа типа: «Вот сыграешь много партий и на опыте поймешь, что это не так; такая формула, я уверен, невозможна» теперь есть возможность ответа другого типа: «Есть такая штука, как нетранзивные шахматные позиции, и они означают, что позиция белых и позиция черных не могут иметь фиксированной количественной оценки без учета друг друга. В круге побед и поражений, где каждая позиция бьет соседку с одной стороны и бьется соседкой с другой, какие могут быть фиксированные численные оценки? Дать тебе готовый пример таких позиций или хочешь придумать свой пример сам?»

Итак, на настоящий момент существование нетранзитивных шахматных позиций — это самое короткое строгое доказательство невозможности независимых друг от друга фиксированных количественных оценок позиций белых и черных.

Что касается заинтересовавшегося взрослого (или ребенка тоже?), то здесь еще много задач: например, поискать ответ на вопрос, на какой минимальной доске (3×3? 4×4?) нетранзитивность позиций уже возможна; построить нетранзитивные позиции в других играх (шашках, го) и так далее. Изобретение объектов, нетранзитивных по превосходству, и придумывание задач с их участием — интересная, а для некоторых даже захватывающая деятельность, объединяющая самые разные области.

1. Н. Резник. Камень, ножницы, бумага // ТрВ-Наука, № 162 от 9 сентября 2014 года.

2. elibrary.ru/item.asp?id=21630164

3. www.nkj.ru/archive/articles/31726/

4. arxiv.org/pdf/1311.6511.pdf

5. bit.ly/2gLbM3R

6. www.microsoft.com/en-us/research/project/non-transitive-dice