Экситоны — искусственные атомы в кристаллах

Казалось бы, что необычного может случиться, если на кристалл упадет свет? Однако пытливый взгляд ученого обнаружит реальное чудо, напоминающее компьютерную игру The Escapists, где узник в конце концов вырывается на свободу, сломав тюремный забор или устроив подкоп.

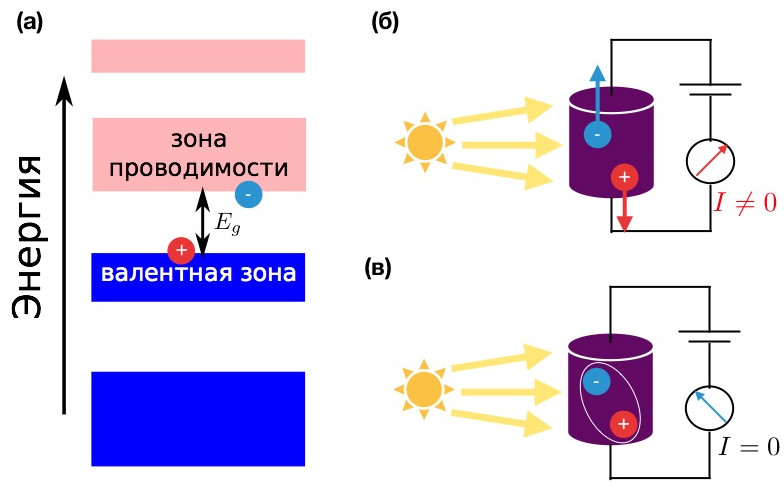
Если энергия падающего на кристалл фотона равна ширине запрещенной зоны (см. нашу врезку с пояснениями) или ее превысит, то электрон под действием света может получить добавочную энергию, преодолеть запрещенную зону, оказаться в зоне проводимости и начать проводить ток. В валентной зоне остается незаполненное состояние — дырка, по­этому и в валентной зоне электроны могут начать движение.

Это — явление фотопроводимости, также называемое внутренним фотоэффектом (именно за фотоэффект Альберт Эйнштейн в 1921 году получил Нобелевскую премию по физике); оно наблюдается во многих кристаллах, как это схематически показано на рис. 1б.

‌

В начале 1930-х годов Яков Ильич Френкель задумался над вопросом: может ли кристалл поглощать свет, но так, чтобы фотопроводимость не возникала, несмотря на наличие электронов и дырок? Ответ на этот, на первый взгляд, парадоксальный вопрос оказался положительным [1]. Действительно, электрон и дырка являются зарядами противоположного знака, поэтому они притягиваются друг к другу и могут образовать связанное состояние. Такое связанное состояние электрона и дырки называют экситоном — квантом «возбуждения» полупроводникового кристалла. Экси­тон — электрически нейтральная квазичастица, поэтому он не может переносить электрический ток.

В модели Френкеля электрон и дырка оказывались на расстоянии порядка межатомного в кристалле — фактически на соседних ионах. Такие экситоны называют экситонами Френкеля или экситонами малого радиуса.

Несколькими годами позже Грегори Ванье и Невилл Мотт [2] поняли, что во многих полупроводниках характерное расстояние между электроном и дыркой может составлять значительное число межатомных расстояний.

Такой экситон — его называют экситоном Ванье — Мотта — является аналогом атома водорода (см. схему на рис. 2а), с той лишь разницей, что эффективная масса экситонного «протона» — дырки — значительно отличается (в меньшую сторону) от массы протона реального. Кроме того, взаимодействующие электрон и дырка находятся в кристалле, где кулоновское взаимодействие ослаблено по сравнению со свободным пространством за счет эффекта экранировки. Однако эти отличия количественные — так же как и для атома водорода, у экситона имеется серия состояний, соответствующих выполнению условий квантования орбит.

Энергии такой серии описываются атомной формулой

E_n= E_g — Ry*/n², (1)

где n = 1, 2, 3… — главное квантовое число, а Ry* — эффективная постоянная Ридберга, которая зависит от параметров кристалла. Она значительно меньше атомного Ридберга и составляет, в зависимости от полупроводника, от тысячных до десятых долей электронвольта. Энергия экситона меньше, чем ширина запрещенной зоны E_g, ведь кулоновское взаимодействие притягивает электрон и дырку, понижая энергию связанного состояния по сравнению с энергией невзаимодействующей пары.

История экспериментального обнаружения экситона весьма драматична. Он был открыт в самом начале 1950-х годов отечественным ученым Евгением Гроссом, блестящим спектроскопистом, и его аспирантом Нури Каррыевым.

Гросс и Каррыев исследовали спектры пропускания света кристаллов закиси меди — Cu₂O (см. фото крис­таллов на рис. 2б) и обнаружили несколько ниже края фундаментального поглощения (соответствующего переходам из валентной зоны в зону проводимости, обсуждавшимся выше) серию узких линий, положения которых неплохо описывались формулой (1). Соответствующий спектр представлен на рис. 2в.

Наличие поглощения на дискретных энергиях было интерпретировано как проявление экситона. Вначале Гросс столкнулся с большим недоверием к своему открытию; его оппоненты пытались приписать эти линии к поглощению за счет примесей или дефектов кристаллов. Более того, в спектре наблюдались линии, соответствующие уровням с n от 2 до 6 или 7 (в зависимости от качества образца), а низшее состояние с n = 1 обнаружить не удавалось. Впрочем, довольно скоро стало понятно, что так и должно быть: основное состояние с n = 1 в закиси меди не вносит вклад в поглощение света за счет особенностей правил отбора. Е. Ф. Гросс и Н. А. Каррыев столкнулись со сложностями при публикации работы (заметка, сообщающая об открытии, вышла в 1952 году в Докладах АН СССР [3]). Говорят, что за свое открытие Гросс был даже на некоторое время понижен в должности.

Последующие исследования, выполненные и Евгением Гроссом с учениками, и другими группами как в Советском Союзе, так и за рубежом, полностью подтвердили открытие экситона. Было подробно исследовано поведение экситона при приложении к кристаллу внешних полей — электрического и магнитного, упругих деформаций; исследованы особенности тонкой структуры спектра экситона. Впоследствии в закиси меди с помощью специальных хитроумных экспериментов был обнаружен и «потерянный» экситон в основном состоянии с главным квантовым числом, равным единице.

После работ Гросса экситоны были обнаружены практически во всех полупроводниках. Все эти факты полностью подтверждали теории Френкеля, Ванье и Мотта. Понятие экситона получило признание. В конце ­1960-х годов Е. Ф. Гросс, обращаясь к участникам Всесоюзного семинара «Экситоны в кристаллах», с радостью отметил, что недоверие к экситону пропало и всё больше физиков подключаются к исследованию этой необычной квазичастицы [5].

С тех пор экситонные эффекты в полупроводниках и полупроводниковых наноструктурах активно исследуются экспериментально и теоретически, ведь именно экситоны во многом определяют оптические свойства полупроводников. Экситоны важны и во многих органических соединениях; сильное экситонное поглощение света открывает перспективы создания приборов для фотовольтаики, эффективно добывающих солнечную энергию.

За почти семьдесят лет, прошедших с момента открытия экситона в закиси меди, интерес сместился к другим полупроводникам. Закись меди — хрупкий материал, поэтому ее применение очень ограниченно (несмотря на красоту кристаллов, их нельзя использовать в ювелирной промышленности, а детекторные приемники радиоволн на Cu2O были вытеснены другими моделями).

В закиси меди с переменным успехом велись поиски бозе-­эйнштейновского конденсата экситонов — коллективного состояния многих квазичастиц, занимающих одно квантовое состояние; для этого исследовалось основное состояние с n = 1, которое сложно найти в спектре, но такой экситон живет долго, так как почти не излучает свет.

Однако недавно, в 2014 году, экситон в закиси меди проявил себя с неожиданной стороны. Экспериментаторы из Технического университета Дортмунда (Германия) смогли значительно продлить серию экситонных состояний и обнаружили экситоны с главным квантовым числом до 25 (рис. 3) [6].

С ростом n кинетическая энергия относительного движения электрона и дырки растет, поэтому они могут разойтись на большее расстояние. Размер экситона тем самым увеличивается с ростом главного квантового числа. У экситона с n = 25 характерный размер составляет около микрона (а у экситона n = 1 — всего лишь несколько нанометров), что очень много по меркам физики полупроводников.

Экситоны с большими квантовыми числами являются аналогами ридберговских атомов (где электрон находится на высоковозбужденной орбите). Такие состояния материи очень интересны для исследователей, ведь это, фактически, макроскопические квантовые объекты, которые эффективно взаимодействуют друг с другом, а также в большой мере подвержены внешним полям. На ридберговских атомах возможны прецизионные эксперименты в области квантовой физии.

Теперь, после обнаружения ридберговских состояний экситонов, появилась возможность изучать аналоги ридберговских атомов в полупроводниках, что значительно облегчает исследования в этой области квантовой физики. Например, из-за наличия кристаллической решетки правила отбора при оптических переходах, связанных с возбуждением экситона, отличаются от атомных, поэтому в спектре ридберговского экситона больше линий — можно одновременно изучать больше состояний.

Появляются новые эффекты, которых нет в физике атомов: например, возбужденные состояния экситона с угловым моментом 3 (состояния f-серии по аналогии с физикой атомов) наблюдаются в спектрах в виде слабых триплетов на высокоэнергетическом краю пиков поглощения [7]. Для экситонов в закиси меди обнаружена «ридберговская» блокада — из-за эффективного отталкивания рядом с одним экситоном второй уже возбудиться не может.

По сравнению с ридберговскими атомами энергии связи ридберговских состояний экситона малы, поэтому экситоны еще более чувствительны к внешним полям. Например, поместив образец закиси меди в плоский конденсатор, можно наблюдать не только многообразие сдвигов, пересечений и антипересечений уровней под действием внешнего электрического поля, но и ионизовать экситон, растащив электрон и дырку электрическим полем в противоположные стороны.

Оказывается, что и тут экситоны ведут себя не так, как ожидалось, — состояния с большим угловым моментом разрушаются в больших электрических полях по сравнению с полями ионизации состояний с меньшим моментом и тем же главным квантовым числом, хотя в нулевом поле их энергии связи меньше [8]. А во внешнем магнитном поле ридберговский экситон в Cu₂O может демонстрировать хаотическое поведение [9].

Вот так, несмотря на свой уже почти 70-летний возраст, экситон в закиси меди ставит перед учеными новые задачи. Перспективы дальнейших исследований можно перечислять очень долго; например, обсуждаются возможности формирования пространственных решеток из ридберговских экситонов [10].

Такие решетки могут использоваться для управления распространением излучения в закиси меди, а в совсем далекой перспективе — для построения «квантовых симуляторов»: систем для моделирования других квантовых систем, которые невозможно реализовать в лабораторных условиях. Ждем новых открытий.

Михаил Глазов, Марина Семина
(ФТИ им. А. Ф. Иоффе, Санкт-Петербург)

1. Frenkel J. On the transformation of light into heat in solids. I // Phys. Rev. 1931. 37. P. 17.
2. Wannier G. H. The structure of electronic excitation levels in insulating crystals // Phys. Rev. 1937. 52. P. 191; Mott On the absorption of light by crystals // Proc. Royal Soc. of London. 1938. A 167. P. 384.
3. Гросс Е. Ф., Каррыев Н. А. Поглощение света кристаллом закиси меди в инфракрасной и видимой части спектра // ДАН СССР. 1952. Т. 84. C. 261.
4. Gross E. F. Optical spectrum of excitons in the crystal lattice // IlNuovo Cimento Series. 1956. 10. 3. P. 672.
5. Пермогоров С. А. V Всесоюзный семинар «Экситоны в кристаллах» (Ленинград, 31 мая — 2 июня 1969 года). // УФН. 1970. 101. C. 341.
6. Kazimierczuk T., Frohlich D., Scheel S., Stolz H., and Bayer M. Giant Rydberg excitons in the copper oxide Cu2O // Nature. 2014. 514. P. 343.
7. Thewes J., Heckötter J., Kazimierczuk T., Assmann M., Froehlich D., Bayer M., Semina M. A., and Glazov M. M. Observation of High Angular Momentum Excitons in Cuprous Oxide // Phys. Rev. Lett. 2015. 115. 027402.
8. Heckötter, Freitag M., Froehlich D., Assmann M., Bayer M., Semina M., and Glazov M. Dissociation of excitons in Cu2O by an electric field // Phys. Rev. 2018. B98. 035150.
9. Assmann M., Thewes J., Frohlich D., and Bayer M. Quantum chaos and breaking of all anti-unitary symmetries in Rydberg excitons // Nature Materials. 2016. 15. P. 741.
10. Poddubny A. N., Glazov M. M., Topological Spin Phases of Trapped Rydberg Excitons in Cu2O, Phys. Rev. Lett. 123, 126801 (2019)