Игра в кубики и колебания мембран

Однажды на каком-то заводе упорно отказывался работать сложный прибор, и ни один специалист не мог ничего поделать. Пришел молодой человек, внимательно осмотрел со всех сторон хитроумное устройство, походил, подумал, почесал затылок, взял обычный молоток, ударил по прибору, и прибор заработал. Человека этого щедро наградили. Но многие удивились, что за удар молотком можно заслужить высокую награду. Тогда им объяснили, что награда выдана не за сам удар, а за знание, куда именно ударить.

Нечто подобное недавно случилось в математике. Наградой стала (среди прочих) премия Европейского математического общества за 2020 год, которая присуждается раз в четыре года десяти исследователям не старше 35 лет в знак признания их выдающегося вклада в математику. В качестве «сложного прибора» выступила (да простит нас неискушенный в математике читатель) «нодальная геометрия решений эллиптических дифференциальных уравнений», «молотком» стали комбинаторно-геометрические соображения, доступные студенту младших курсов, а молодого человека звали Александр Логунов.

Теперь обо всем по порядку. Истоки нодальной геометрии восходят к опытам Гука и Хладни, в которых мелкий песок, насыпанный на колеб­лющуюся пластинку, собирался в узловые линии, образующие причудливые узоры, зависящие от формы пластины и частоты колебания. Эти линии состоят из точек пластины, которые остаются неподвижными. Читатель найдет многочисленные иллюстрации этих опытов, набрав в Google «фигуры Хладни».

Разнообразные вопросы об узловых линиях, возникающих при колебаниях, интригуют ученых более 200 лет. Премия, полученная Александром Логуновым, была не первой наградой за работы в этой области. Еще в 1809 году после визита Хладни в Париж Французская академия наук объявила конкурс, целью которого было «построить математическую теорию упругих поверхностей и указать, насколько она согласуется с опытными данными». Премия была выдана в 1816 году Софи Жермен, а законченную математическую модель немного позднее построил Густав Кирхгоф.

Следует отметить, что более непосредственное отношение к работам Логунова имеет теория колебаний не жестких пластин, а гибких упругих мембран (отличие в том, что мембрана сопротивляется только растяжению, а пластина дополнительно еще и изгибанию и сжатию, что приводит к более сложной математической модели). Мембрана при этом может быть любой формы: плоской с закрепленными краями, сферической, в виде бублика и т. п., может быть и многомерной.

Согласно одному из основных принципов теории малых колебаний функция, описывающая отклонение мембраны от положения равновесия, представляется в виде наложения (т. е. суммы) простейших собственных колебаний. Каждое собственное колебание происходит с определенной частотой $\omega$ и описывается математически произведением $\cos(2\pi\omega t)v_{\omega}(x)$, где $t$ — время, а $v_{\omega}(x)$ — так называемая собственная функция, зависящая лишь от точки х мембраны.

С точки зрения дифференциальных уравнений собственные функции $v_{\omega}$ есть решения уравнения $ \Delta v_\omega+4\pi^2\omega^2v_\omega=0 $, а узловые линии (множества, в размерности 3 и выше) — это просто точки $х$, удовлетворяющие условию $v_\omega(x)=0$. Символом $\Delta$ здесь обозначен вездесущий оператор Лап­ласа, явное выражение для которого зависит от выбранной системы координат и упругих свойств мембраны.

В случае плоской однородной мембраны, представленной в обычных декартовых координатах, он имеет вид $\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}$. Приведенное выше уравнение для собственных функций оператора Лапласа возникает повсеместно и в других разделах математики и физики, от геометрии и теории вероятностей до квантовой механики. Поэтому неудивительно, что поведение собственных функций и их узловых линий является объектом пристального изучения. Несмот­ря на это, многие задачи остаются нерешенными до сих пор.

По-видимому, самой известной из задач об узловых множествах стала гипотеза Яу Шинтуна об их размере, высказанная более 40 лет назад. Она утверждает, что этот размер (длина в размерности 2, площадь в размерности 3 и т. д.) всегда растет как линейная функция частоты $\omega$. В случаях, когда колеблющаяся мембрана обладает дополнительными симметриями, собственные функции иногда удается найти в явном виде. В отсутствие симметрий для собственной функции невозможно написать явное выражение, и для оценки размера узлового множества обычно разбивают мембрану на маленькие квадратики, оценивают размер в каждом из них, а потом складывают результаты.

Было замечено, что удобным инструментом для таких оценок является индекс удвоения $N(Q)=\ln\frac{\max_{2Q}|v_\omega|}{\max_Q|v_\omega|}$, измеряющий, насколько быстро увеличивается максимум модуля функции при переходе от куба $Q$ к кубу $2Q$ с тем же центром, но вдвое большей стороной. Полезным является такой факт: если индекс удвоения остается ограниченным, то ограничен и размер части узлового множества, попавшей в куб $Q$.

Первое значительное продвижение в гипотезе Яу получили около 30 лет тому назад Харольд Доннелли (Harold Donnelly) и Чарльз Фефферман (Charles Fefferman). Они доказали, что для любого квадрата индекс удвоения собственной функции оценивается сверху частотой колебания. Следующее продвижение в этом круге задач принадлежит Николаю Надирашвили. Он заметил, что вопросы, заданные Яу Шинтуном, могут быть сведены к близким вопросам для существенно более простого класса гармонических функций. Так называются решения уравнения $\Delta v=0$ (они описывают стационарные состояния мембран). Среди вопросов Надирашвили был, например, такой: верно ли, что любая непостоянная гармоническая функция в трехмерном пространстве обращается в ноль на множестве бесконечной площади? (Аналогичное утверждение на плоскости является несложным упражнением.) На протяжении 25 лет столь невинный вопрос об одном из центральных математических объектов оставался открытым.

После работ Доннелли, Феффермана и Надирашвили стало ясно, что принципиальным является вопрос о том, что происходит с индексом удвоения гармонической функции при измельчении квадрата (или куба в больших размерностях) на мелкие кусочки. Несмотря на усилия многих математиков, никакого продвижения в этом вопросе не было до появившихся в 2016 году работ Александра Логунова и Евгении Малинниковой.

В их основе лежала следующая изящная комбинаторная лемма (мы ограничимся лишь плоским случаем, уже содержащим основные трудности). Пусть гармоническая функция имеет большой индекс удвоения $N$ в единичном квадрате. Тогда, если нарезать этот квадрат на $A^2$ достаточно маленьких квадратиков одинакового размера, то не более чем в $A/2$ из них индекс удвоения может превысить $N/2$. Эта лемма привела к доказательству упомянутой выше гипотезы Надирашвили и части гипотезы Яу, а чуть позднее — к доказательству того, что длина узловых линий собственного колебания однородной плоской мембраны, зажатой на краю, растет как линейная функция частоты.

В заключение несколько слов о самом Александре Логунове. Александр вырос в Перми и в Санкт-Петербурге. Как и многие петербургские математики, он окончил одну из математических школ города (239-ю). В 2015 году он защитил кандидатскую диссертацию, выполненную под руководством Виктора Петровича Хавина. После двух лет, проведенных в Тель-Авиве, Александр перебрался в Принстон, где работает до настоящего времени. Он по-прежнему регулярно навещает и Санкт-Петербург, и Тель-Авив и успешно продолжает решать другие, столь же трудные и увлекательные, задачи.

↑

«Я занимаюсь нодальной геометрией»

Александр Логунов, Assistant professor Принстонского университета (США), ответил на несколько вопросов нашей газеты.

— Как вы решили прий­ти в математику? Были ли сомнения в выборе?

— Будучи школьником 12 лет, я случайно попал в замечательный математический кружок при физико-математическом лицее № 239 Санкт-Петербурга, который сыг­рал огромную роль в моем образовании. Я до сих пор поддерживаю контакт с этой крайне успешной системой кружков и олимпиад. На первом курсе я получил разрешение учиться одновременно на двух направлениях: математика и экономика. Через две недели после начала занятий мне стало очевидно, что мое, а что нет.

— Как бы вы описали область ваших математических интересов?

— Анализ (наука о неравенствах), геометрия, математическая физика.

— Не могли бы вы в научно-популярном формате (нас читают не только физики, но и филологи) описать тот результат, который был отмечен премией Европейского математического общества?

— В представлении к премии нигде об этом не говорится. Последние пять лет я занимаюсь нодальной геометрией.

Термин «нодальные множества» придумали физики для обозначения удивительных линий, отчетливо видных, например, в эксперименте Хладни, в котором по металлической пластинке проводят смычком, и она резонирует.

На нодальные множества обратили внимание независимо друг от друга такие физики, как Леонардо да Винчи, Галилео Галилей, Роберт Гук, а систематически изучал и описал их Эрнст Хладни. Наполеон был так впечатлен резонансным экспериментом Хладни, что предложил Французской академии наук назначить премию за лучшее математическое объяснение этого эксперимента. После назначения премии французские физики и математики годами спорили, каким же уравнением описываются нодальные множества.

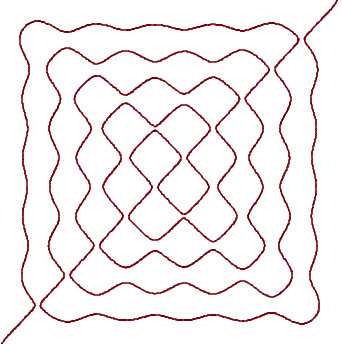
В 1816 году премию получила Софи Жермен (Marie-Sophie Germain, 1776–1831). Благодаря ей мы знаем, что нодальные множества — это нули решений эллиптических уравнений, которые математики изучают и пытаются объяснить на абстрактном уровне. Про нодальные множества можно легко придумывать математические вопросы — надо просто смотреть на картинки, которые сделали физики, и пытаться доказать или опровергнуть то, что глазами видно. Самый известный вопрос — это гипотеза Яу (в честь Яу Шинтуна), которая говорит, как связана длина нодальных линий с частотой.

Рис. Д. Беляева и А. Логунова

Редакция благодарит Дмитрия Беляева за любезно предоставленные иллюстрации