Космологический ликбез. Что такое Вселенная

MathJax.Hub.Config({ tex2jax: { inlineMath: [[‘$’,’$’], [«\\(«,»\\)»]] } });

Мы в соавторстве с Валерием Рубаковым работаем над книгой с рабочим названием «Острые углы космологии». Она будет во многом полемической: рассмотрим основные темы, о которых спорят и судачат, и вопросы, ответы на которые пока еще не знают. Но для начала — ликбез. Это первая глава будущей книги.

Разные люди понимают под словом «Вселенная» совершенно разные вещи. Например, «всё сущее». Но надо бы сузить понятие, до­определить его до чего-то конкретного. Большинство космологов, вероятно, согласится с тем, что Вселенная — это пространство со всем содержимым, в котором мы находимся и которое теоретически можно покрыть непрерывной гладкой координатной сеткой, или мысленной сетью наблюдателей, каждый из которых видит соседей.

Вселенная имеет четыре измерения — три одинаковых (пространство) и четвертое — радикально отличающееся от этих трех (время).

Это Вселенная с большой буквы, но для понимания Мироздания нам потребуется вселенная с маленькой буквы. Это то же самое, только надо исключить оттуда нас и убрать конкретное число измерений. Получим некое другое пространство, в котором нас нет, пространство с другим содержимым и, возможно, с другими свойствами, включая число и характер измерений. Это будет просто другая вселенная, которую мы никогда не сможем наблюдать, можем только сказать, что ничто не запрещает существование ее и ей подобных. И еще есть некоторые наводящие соображения, по которым такие вселенные должны быть, причем в неограниченном количестве, в том числе непохожие на нашу.

Геометрия Вселенной

Какова геометрия Вселенной? Легче всего представить себе бесконечное вечное пространство, в котором работают аксиомы Евклида, — так Вселенную и представляли себе до третьей декады ХХ века. Но это не обязательно так. Представим себе двумерное пространство — это легко. Например, бесконечную плоскость, где также справедливы аксиомы Евклида. Это будет двумерный аналог бесконечного евклидова трехмерного пространства. Но можно легко представить и иной вариант — сферу. Это замкнутое конечное пространство, где параллельные прямые пересекаются, а сумма углов треугольника больше 180°. Такое пространство называется римановым, его кривизна положительна.

Представим себе, что эта сфера — целый мир, вселенная с маленькой буквы. По сфере распространяется свет — по геодезическим линиям, т. е. по кратчайшему расстоянию между точками. На сфере существуют двумерные материальные объекты и даже созданные из них разумные существа. Эта вселенная не имеет краев, но она конечна — пространство замкнуто. Если вселенная стационарна, т. е. ее размер и форма не меняется со временем, то в ней можно совершить кругосветное путешествие — отправиться по прямой и вернуться с обратной стороны. В этом случае яркие объекты можно увидеть с двух противоположных сторон, подобно тому, как ударная волна от мощнейшего взрыва приходит дважды, обогнув земной шар в противоположных направлениях.

Мы, живущие в трех измерениях, видим сферу со стороны, видим, что она выпуклая и замкнутая. А могут ли микроскопические двумерные существа, живущие на этой сфере и не имеющие выхода за ее пределы, убедиться, что она не плоская? Еще как! Например, построить большой треугольник и измерить сумму углов. Если она больше 180° — то кривизна положительна, геометрия риманова, и можно говорить о том, что их вселенная замкнута (в предположении, что кривизна везде одинакова). А если сумма равна 180° или меньше, значит, кривизна нулевая или отрицательная, геометрия евклидова или Лобачевского, вселенная бесконечна. Причем даже не обязательно «строить» треугольник — достаточно измерить угловой размер объекта с известным линейным размером и известным расстоянием до него.

В нашем примере предполагается, что есть дополнительное третье измерение, иначе мы бы не могли смотреть на сферу со стороны. Но может ли его не быть вовсе? Конечно, может! Существование такой двумерной вселенной без всяких дополнительных измерений не противоречит никаким принципам. А может ли быть так, что измерений все-таки три, а вселенная — просто вложенный в них двумерный пузырь, из которого нельзя или очень трудно выпрыгнуть в третье измерение — физика не позволяет? Тоже может быть — это называется «мир на бране». Теоретики рассматривают возможность, что наша Вселенная — тоже мир на бране, но проверить, так ли это, мы пока не можем.

Теперь следующий, более трудный, но важный шаг: пусть наша сфера будет трехмерной — трехмерное замкнутое пространство. Это вообразить гораздо сложнее, поскольку мы не можем представить себе четвертое измерение, помогающее взглянуть извне на трехмерную сферу. Теперь мы сами — те микроскопические существа, заключенные в замкнутом пространстве. Если наша вселенная стационарна (радиус сферы не меняется со временем), мы можем совершить кругосветное путешествие, отправившись в любом направлении и вернувшись с противоположного. Мы будем видеть яркие объекты с двух противоположных сторон неба (такие объекты безуспешно искались). И если сфера совсем идеальная, то взгляд, брошенный человеком в любом направлении, упрется в его же затылок, правда, его изображение будет исчезающе тусклым из-за колоссального увеличения.

До сих пор мы говорили о вселенной как о замкнутой сфере идеальной формы. Это не обязательно так. Сфера может быть покрыта мелкой рябью, может иметь глобальные деформации (что усложняет кругосветное путешествие). Теоретически вселенная может даже иметь другую топологию, например тороидальную. Но все-таки нам важно, чтобы вселенная была замкнутой и конечной. Теоретически можно описать и бесконечную вселенную, но тогда встает тяжелый вопрос: как она могла появиться? Этот вопрос можно просто проигнорировать, но с конечной вселенной намного проще: вопрос о ее появлении (и размножении) не то, чтобы решен, но просматривается в общих чертах.

А может ли вселенная иметь форму чемодана? То есть быть пространством не замкнутым, а ограниченным какими-то стенками? Теоретически — да. Например, есть такое понятие, как «доменные стенки», разделяющие пространства с разными законами физики. Тогда за стенкой лежит другая смежная вселенная (домен) и скорее всего стенка движется — один домен пожирает другой, но это уже за пределами темы этой книги, и возвращаться к доменным стенкам мы не будем.

Вариантов геометрии вселенных огромное множество, но мы должны остановиться на самом простом, который к тому же и самый естественный: однородная изотропная сфера. Однородная означает, что условия в каждой точке одинаковы, изотропная — нет выделенных направлений. В случае нашей Вселенной — сфера трехмерная. Для демонстрации будем использовать идеальную двумерную сферу в трехмерном пространстве. Мы приходим к тому, что называется пространственно ноль-мерной задачей: ото всех пространственных координат ничего не зависит, независимой переменной остается только время. Решение задачи будет описывать только размер (радиус кривизны, масштаб) Вселенной — его изменение со временем.

Кинематика Вселенной

Выше мы для наглядности рассматривали стационарную вселенную. На самом деле так не бывает. Устроить стационарную вселенную очень трудно — нужна точная подгонка параметров, об этом будет сказано ниже. Реальные вселенные либо расширяются, либо сжимаются. Нам интереснее первый вариант, поскольку наша Вселенная расширяется.

Кругосветное путешествие нам не светит: никто, ограниченный скоростью света, не сможет обогнать расширение Вселенной, поскольку оно может быть сверхсветовым, а в нашей Вселенной — точно сверхсветовое. Это не ошибка — удаленные области Вселенной действительно разлетаются со скоростями выше световой. Как ни крамольно это звучит. Чтобы объяснить этот парадокс, нужно сначала разобраться в том, что значит «расширение» и «удаленные области разлетаются». Эти слова подразумевают, что во вселенной в каждой точке существует некоторая выделенная система отсчета.

В нашей модели вселенной в виде двумерной поверхности замкнутой сферы расширение можно смоделировать, например, надувая эту сферу, если она резиновая. Там выделенная система отсчета очевидна — это материал сферы. Пусть резина везде одинаковая и можно нанести на нее точки и наблюдать, как они удаляются друг от друга при надувании. А в реальной физической Вселенной вроде бы нет материала, выделяющего систему отсчета. В пространстве действует специальная теория относительности, отрицающая существование выделенных систем. Ну да, есть малоподвижные звезды и галактики, но это лишь факт биографии нашей Вселенной, в специальной теории относительности они не задают систему отсчета. А в общей теории относительности, оказывается, задают.

Выделенной системы отсчета нет только в пустом плоском пространстве. А если пространство не пустое? Значит, появляется система, где суммарный импульс вещества равен нулю (назовем ее «система объемного покоя»). Эта система — факт биографии вселенной, но общая теория относительности вынуждена с этим фактом считаться — для этой системы уравнения общей теории относительности выглядят несравненно проще, и их решения интерпретируются однозначно: сжимается или расширяется само пространство. Если вселенная однородна и изотропна, ее эволюция определяется изменением одной переменной. Это так называемый масштабный фактор a. Если пространство кривое, то в качестве естественного масштабного фактора можно взять радиус кривизны. Если пространство настолько плоское, что его кривизна лежит за пределами обнаружимости, тогда удобней использовать безразмерный масштабный фактор: расстояние между двумя точками пространства относительно расстояния между ними же в фиксированный момент времени. То есть берем расстояние между точками A и B в определенный момент времени (например, сейчас в нашей Вселенной), обозначаем его a_o и смотрим, как меняется расстояние a(t) между этими точками со временем. Для удобства убираем конкретное расстояние между конкретными точками, работая с безразмерным соотношением, общим для всей однородной вселенной, a(t)/a_o, где t — время. Тогда относительный темп расширения вселенной будет ȧ/a, где ȧ — производная a(t) по времени — это ни что иное, как постоянная Хаббла, H. В странных единицах, к которым все привыкли, постоянная Хаббла для нашей Вселенной в настоящий момент примерно равна 67 км/с на мегапарсек. Если обратить внимание на то, что расстояние входит как в числитель, так и в знаменатель, можно его сократить, выразив мегапарсек в километрах. Получим 2,2 ⋅ 10^–18 с^–1 (обратная величина — порядка возраста Вселенной, что не случайно). Скорость, с которой точки А и В удаляются друг от друга, равна S ⋅ Н, где S — расстояние между точками в данный момент. Если S = c/H ~ 1,4 ⋅ 10²⁸ см, то точка В удаляется от точки А со скоростью света.

Что такое горизонт вселенной? По идее, это расстояние между точками А и В (под расстоянием понимаем сумму длин малых отрезков, измеренных в сопутствующей системе отсчета по пути от А к В), когда нечто произошедшее в одной точке может повлиять на происходящее в другой точке, но не дальше. Но здесь, в отличие от ситуации с черной дырой, которая тоже имеет горизонт, возникает важный вопрос «когда?». Когда произошло и когда повлияло. Есть два определения горизонта:

1. Событие произошло когда-то в прошлом, повлияло сейчас (событие и влияние могут быть испусканием и получением светового сигнала). Момент в прошлом выбирается так, чтобы сейчас точки, обменявшиеся причинно-следственным влиянием, разлетелись на максимальное расстояние (для нашей Вселенной этот момент будет Большим взрывом). Это так называемый горизонт частиц. Он неплохо вычисляется, поскольку мы знаем историю Вселенной.
2. Событие произошло сейчас и когда-то в будущем повлияет на точку В, но не дальше. Это так называемый горизонт событий. Мы не знаем, где он и существует ли он вообще, поскольку не знаем будущего Вселенной. Когда говорят просто «горизонт», почти всегда имеют в виду первый вариант, т. е. горизонт частиц.

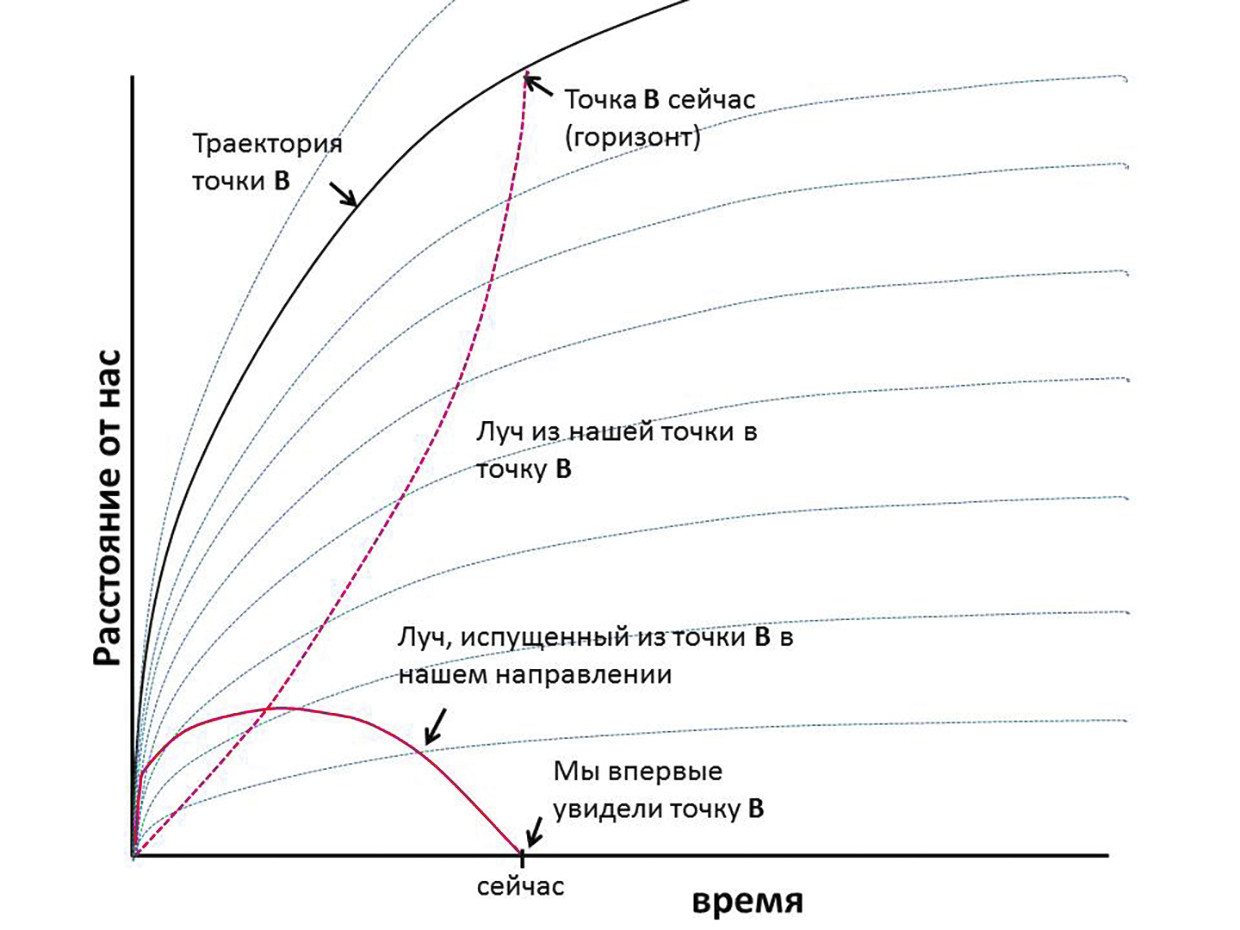
Горизонт нашей Вселенной в настоящий момент находится в 46 млрд световых лет от нас при возрасте Вселенной 13,8 млрд лет. Ничего удивительного: точка В в молодой Вселенной убегала от нашей точки А гораздо быстрей света. Более того, фотон, испущенный из точки В в сторону А, тоже удалялся от точки А быстрей света. Ситуацию приблизительно иллюстрирует рисунок внизу.

Не будет большой ошибки, если мы выберем точку В не в момент Большого взрыва, а чуть позже — в момент рекомбинации. От момента Большого взрыва до нас не дошло ничего, кроме нейтрино и гравитационных волн, а от момента рекомбинации дошло реликтовое излучение, у нас есть прекрасная карта Вселенной возраста 380 тыс. лет. И мы видим там зародыши будущей крупномасштабной структуры — будущие войды и вероятные будущие сверхскопления. Сейчас всё это улетело на 46 млрд световых лет, но у нас есть хотя бы приблизительная информация о том, что там сейчас находится. В этом и есть смысл горизонта.

А откуда берется красное смещение? Что происходит с фотоном по пути? Первая реакция обычного человека — приписать красное смещение эффекту Доплера. Галактика N удаляется от нас из-за расширения Вселенной, и ее спектр смещен в красную сторону на величину $\frac{(1-v/c)}{\sqrt{1-v^2/c^2}}$. Если галактика неподалеку, то всё в порядке, эффект Доплера дает разумный результат. А если галактики очень далеко, и это даже не галактика, а некая точка В с графика в молодой Вселенной, когда она удалялась быстрее света? Что ставить в формулу для эффекта Доплера? Скорость, превышающую световую? И что произойдет со знаменателем в этой формуле? Между тем мы видим реликтовое излучение с красным смещением около тысячи. Откуда взялась такая величина?

Дело в том, что природа космологического красного смещения другая — это именно расширение пространства. Волна электромагнитного поля, пересекающая пространство, растягивается вместе с ним. Если за время пролета вселенная растянулась в a раз, то и длина волны увеличится в a раз, а ее частота и энергия в a раз упадет. Наша Вселенная с момента рекомбинации растянулась примерно в тысячу раз, соответственно энергия фотонов и температура реликтового излучения в тысячу раз уменьшилась. Кстати, если рассмотреть покраснение фотонов как череду небольших доплеровских смещений в расширяющемся пространстве, разбив его траекторию на небольшие шаги, мы получим тот же самый результат.

Можно продемонстрировать растягивание электромагнитной волны вместе с расширением вселенной и более строго, но это потребует введения дополнительных понятий и формул. Частицы, летящие со скоростью, близкой к скорости света, тоже теряют свою энергию как Е = Е_о⋅ a_o/a(t), а нерелятивистские частицы таким же образом теряют скорость относительно системы покоя.

А как же специальная теория относительности? Она никуда не делась, просто надо помнить, что преобразования Лоренца глобально «в лоб» применимы для плоского (евклидова) стационарного пространства. А в расширяющемся или кривом пространстве они тоже применимы, но имеют локальный характер: все преобразования скоростей и другие релятивистские эффекты сохраняют свой вид для событий, относительно близких в пространстве.