Математика малых доз

Одиночные редкие события плохо поддаются статистическому анализу, поскольку каждая случайная реализация события уникальна. Если же мы наблюдаем необычные статистически воспроизводимые закономерности, то возникает желание объяснить их некоторой специально организованной структурой исследуемого объекта.

Спектры поглощения растворов редких случайных макромолекулярных кластеров демонстрируют вполне регулярную, устойчивую иерархическую структуру, которую легко можно принять за проявление специальной внутренней организации исследуемых кластеров при изучении вещества, присутствующего в среде в области сверхнизких концентраций.

На самом деле наблюдаемые статистические закономерности с весьма причудливым регулярным поведением обусловлены проявлением теоретико-числовой структуры редких случайных событий и не требуют привлечения неконтролируемых физических соображений для их объяснения.

Мне очень нравится читать комментарии к популярным статьям, посвященным обсуждению такой волнующей умы людей темы, как гомеопатия: после обмена несколькими пробными мнениями, которые напоминают разведку боем перед артобстрелом, авторы комментариев немедленно переходят к обсуждению личностей друг друга, практически позабыв о сюжете. При этом по глубине высказанных мнений дискуссия очень быстро начинает походить на беседу Остапа Бендера с ксендзами из «Золотого теленка»: «Бога нет», — сказал Остап. «Бог есть», — сказали ксендзы…

Среди адептов гомеопатии бытует мнение, что эффект гомеопатического средства увеличивается по мере уменьшения концентрации действующего начала. Это утверждение, которое, как мне кажется, отражает суть гомеопатии, наиболее выпукло сформулировано в шутке: «…Больной перестал принимать препарат и умер от передозировки…» Эффект лечения гомеопатическим препаратом оценивается исключительно субъективно в терминах «Больной X выздоровел» или «Больному Y стало лучше (хуже)».

Как физику мне всё время хочется спросить: «Господа, а можно ли измерить какое-нибудь действующее начало гомеопатического средства in vitro?» Приверженцам гомеопатии, возможно, ответ известен, но будучи сакральным, он скрыт от случайного взгляда посторонних. На допросе с пристрастием гомеопаты держатся стойко, не выдавая тайны, объясняя гомеопатический эффект «памятью воды», «информационным полем», иногда даже апеллируя к квантовой механике.

С точки зрения современной науки словосочетания «память воды», «информационное поле» являются не чем иным, как заклинаниями, имеющими не больший смысл, чем, скажем, «торсионные поля», «вечный нанодвигатель» или «космофизические факторы». Дефект логических построений приверженцев «нетрадиционной науки» заключается в том, что необъясненные явления они пытаются «объяснить» с помощью понятий, которые сами оказываются «вещью в себе». Связка «непонятое явление — объяснение», которая претендует на научность, с необходимостью должна удовлетворять двум условиям. Первое: обсуждаемое явление должно быть досконально проверено в независимых экспериментах. Эти эксперименты должны давать статистически достоверные одинаковые результаты, которые исключают как «человеческий фактор» (то есть роль самого экспериментатора в опыте), так и роль всех неконтролируемых внешних условий. Второе: теория, описывающая явление, сколь бы новой и революционной она ни была, должна корнями уходить в существующее представление об устройстве мира.

Вернемся к гомеопатии. Итак, концентрация действующего начала гомеопатического средства в лекарственном препарате такова, что его там просто нет, поэтому измерять собственно нечего. Но тут на выручку гомеопатам приходят химики и биологи, которые говорят: а мы зафиксировали физиологический эффект действия сверхмалых доз! В растворе вещество присутствует, правда, в ничтожных количествах и тем не менее оно действует на живые организмы! О физиологическом действии мы говорить не будем, так как хотим определить физический эффект именно вне биологического организма, но раз вещество все-таки присутствует, можно попытаться изучить его молекулярную структуру, поставив соответствующие эксперименты, например исследовав спектр поглощения раствора данного вещества на разных частотах.

Я отвлекусь на один абзац от основной темы и попробую кратко объяснить, почему резонансный спектр поглощения несет информацию о структуре растворенного вещества. Классическая работа М. Каца 1966 года Can one hear the shape of the drum? («Можно ли услышать форму барабана?») была посвящена исследованию такого вопроса.

Пусть есть контур произвольной формы, на который натянута упругая пленка. Можно ли по спектру собственных колебаний пленки узнать форму контура? Ответ на этот вопрос таков: по спектру можно узнать площадь поверхности, длину периметра и топологическую связность (количество дырок в поверхности), но форму узнать нельзя. Тем не менее информация, извлекаемая из спектра собственных колебаний упругой мембраны, достаточно обширная. Аналогичный вопрос можно задать в отношении молекулы достаточно сложной конфигурации, которую с определенной натяжкой (в так называемом гармоническом приближении) можно представлять в виде графа, сделанного из пружинок, как это изображено на рис. 1 слева.

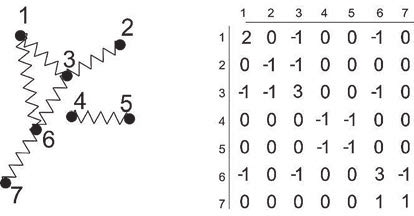
Для определения спектра собственных колебаний таких молекул нужно сконструировать лапласовскую матрицу A={a_ij}, которая соответствует ансамблю графов и построена по следующим правилам: если частицы с номерами i и j (i≠j) соединены пружинка ми, то a_ij = –1, в противном случае a_ij = 0. На диагонали (то есть для матричных элементов a_ii) нужно поставить сумму значений в строке с обратным знаком, как это показано на рис. 1 справа.

Вычисляя собственные значения матрицы A, мы можем извлечь информацию о внутреннем устройстве соответствующего ансамбля молекул. Реализовать такой эксперимент можно, взяв, например, лазер с перестраиваемой частотой и облучив раствор молекул на разных частотах. Измеряя спектр поглощения раствора на частоте λ, мы получим гистограмму резонансных частот ρ(λ), которая говорит о том, сколько раз в спектре молекулы встретилась частота колебаний λ.

Итак, определение спектра поглощения — это удобный способ протестировать молекулярную структуру агрегатов вещества, помещенного в низкомолекулярный растворитель. Представьте себе теперь, что некто, работая со сверхнизкими концентрациями вещества в воде, получил устойчивую иерархическую самоподобную структуру ρ(λ) с периодически повторяющимися максимумами типа изображенной на рис. 2.

Какой вывод о структуре молекул хочется сделать, глядя на этот рельеф? Первое предположение, приходящее в голову, таково: сложная структура резонансов обусловлена сложной внутримолекулярной организацией молекул образца, а периодичность связана с характерными структурными особенностями макро-молекулярных агрегатов.

В действительности оказывается, что это совсем не так. Сложная структура гистограммы ρ(λ) с завидным постоянством повторяется для любых редких макро-молекулярных агрегатов и тем самым никоим образом не связана с их внутренней организацией. Для проверки этого утверждения мы генерировали много матриц А типа изображенной на рис. 1 со случайным очень редким расположением ненулевых элементов a_ii, для каждой матрицы определяли набор собственных частот, усредняли по большому количеству разных матриц и строили соответствующие гистограммы ρ(λ).

Каждый раз мы получали одну и ту же картину с одним и тем же расположением пиков. У дотошного читателя может возникнуть вопрос: не связана ли эта повторяемость с дефектом генератора случайных чисел, который используется для того, чтобы строить разные матрицы A? Ответ: нет, не связана. Зависимость, изображенную на рис. 2, можно вычислить теоретически, не прибегая к компьютерным расчетам. В результате можно показать, что последовательности максимумов, наиболее медленно монотонно убывающих по высоте (как, например, последовательность 1, 2, 3, 4, … на рис. 2), образуют так называемые последовательности Фарея, хорошо известные в теории чисел.

Итак, образно говоря, любая макро-молекулярная неструктурированная грязь в достаточно малых количествах, находящаяся в большом объеме низкомолекулярного растворителя, даст повторяющийся четкий сигнал, изображенный на рис. 2. С уменьшением концентрации грязи максимумы будут постепенно становиться всё ниже и ниже, но при этом их положение останется неизменным. В конце концов в чистом растворе останется один центральный пик, который отвечает мономолекулярной среде (все собственные значения λ лапласовской матрицы равны 0).

Мне хотелось бы отметить, что обсуждаемая возможность получить «нечто из ничего» отнюдь не перечеркивает исследований, касающихся биологической активности сверхмалых концентраций макромолекулярных веществ. Пример, приведенный выше, — это предостережение математиков для физиков, химиков и в первую очередь биологов: будьте внимательны при работе с малыми концентрациями веществ, поскольку в этих условиях обычный шум выглядит совсем необычно и желаемое может быть с легкостью принято за действительное при недостаточно глубоком анализе данных физических измерений. Итак, подведем итог. Коллективное проявление случайных некоррелированных событий может быть весьма сложным и иметь весьма причудливую функцию распределения, состоящую из перемежающихся максимумов и минимумов, положение которых на горизонтальной оси определяется исключительно теоретико-числовыми закономерностями, не имеющими никакого отношения к специфической внутренней организации макромолекулярных кластеров. Таким образом, работая с системами в области очень низких концентраций, коллективную статистику редких событий следует аккуратно учитывать, для того чтобы четко отделять полезный сигнал от шума.

Я хотел бы закончить данный текст, вспомнив бритву Оккама: «Не нужно множить сущности без необходимости». Поиск объяснения сложных закономерностей нужно начинать с наиболее простых и прозрачных соображений.